Various contrastive learning approaches have been proposed in recent years and achieve significant empirical success. While effective and prevalent, contrastive learning has been less explored for time series data. A key component of contrastive learning is to select appropriate augmentations imposing some priors to construct feasible positive samples, such that an encoder can be trained to learn robust and discriminative representations. Unlike image and language domains where “desired” augmented samples can be generated with the rule of thumb guided by prefabricated human priors, the ad-hoc manual selection of time series augmentations is hindered by their diverse and human-unrecognizable temporal structures. How to find the desired augmentations of time series data that are meaningful for given contrastive learning tasks and datasets remains an open question. In this work, we address the problem by encouraging both high fidelity and variety based upon information theory. A theoretical analysis leads to the criteria for selecting feasible data augmentations. On top of that, we propose a new contrastive learning approach with information-aware augmentations, InfoTS, that adaptively selects optimal augmentations for time series representation learning. Experiments on various datasets show highly competitive performance with up to 12.0% reduction in MSE on forecasting tasks and up to 3.7% relative improvement in accuracy on classification tasks over the leading baselines.
Time series data in the real world is highly dimensional, unstructured, and complex with unique properties, leading to challenges for data modeling (Yang and Wu 2006). In addition, without human recognizable patterns, it is much harder to label time series data than images and languages in real-world applications. These labeling limitations hinder deep learning methods, which typically require a huge amount of labeled data for training, being applied on time series data (Eldele et al. 2021). Representation learning learns a fixed-dimension embedding from the original time series that keeps its inherent features. Compared to the raw time series data, these representations are with better transferability and generalization capacity. To deal with labeling limitations, contrastive learning methods have been widely adopted in various domains for their soaring performance on representation learning, including vision, language, and graph-structured data (Chen et al. 2020; Xie et al. 2019; You et al. 2020). In a nutshell, contrastive learning methods typically train an encoder to map instances to an embedding space where dissimilar (negative) instances are easily distinguishable from similar (positive) ones and model predictions to be invariant to small noise applied to either input examples or hidden states.
Despite being effective and prevalent, contrastive learning has been less explored in the time series domain (Eldele et al. 2021; Franceschi, Dieuleveut, and Jaggi 2019; Fan, Zhang, and Gao 2020; Tonekaboni, Eytan, and Goldenberg 2021). Existing contrastive learning approaches often involve a specific data augmentation strategy that creates novel and realistic-looking training data without changing its label to construct positive alternatives for any input sample. Their success relies on carefully designed rules of thumb guided by domain expertise. Routinely used data augmentations for contrastive learning are mainly designed for image and language data, such as color distortion, flip, word replacement, and back-translation (Chen et al. 2020; Luo et al. 2021). These augmentation techniques generally do not apply to time series data. Recently, some researchers propose augmentations for time series to enhance the size and quality of the training data (Wen et al. 2021). For example, TS-TCC (Eldele et al. 2021) and Self-Time (Fan, Zhang, and Gao 2020) adopt jittering, scaling, and permutation strategies to generate augmented instances. Franceschi et.al. propose to extract subsequences for data augmentation (Franceschi, Dieuleveut, and Jaggi 2019). In spite of the current progress, existing methods have two main limitations. First, unlike images with human recognizable features, time series data are often associated with inexplicable underlying patterns. Strong augmentation such as permutation may ruin such patterns and consequently, the model will mistake the negative handcrafts for positive ones. While weak augmentation methods such as jittering may generate augmented instances that are too similar to the raw inputs to be informative enough for contrastive learning. On the other hand, time series datasets from different domains may have diverse natures. Adapting a universal data augmentation method, such as subsequence (Xie et al. 2019), for all datasets and tasks leads to sub-optimal performances. Other works follow empirical rules to select suitable augmentations from expensive trial-and-error. Akin to hand-crafting features, hand-picking choices of data augmentations are undesirable from the learning perspective. The diversity and heterogeneity of real-life time series data further hinder these methods away from wide applicability.
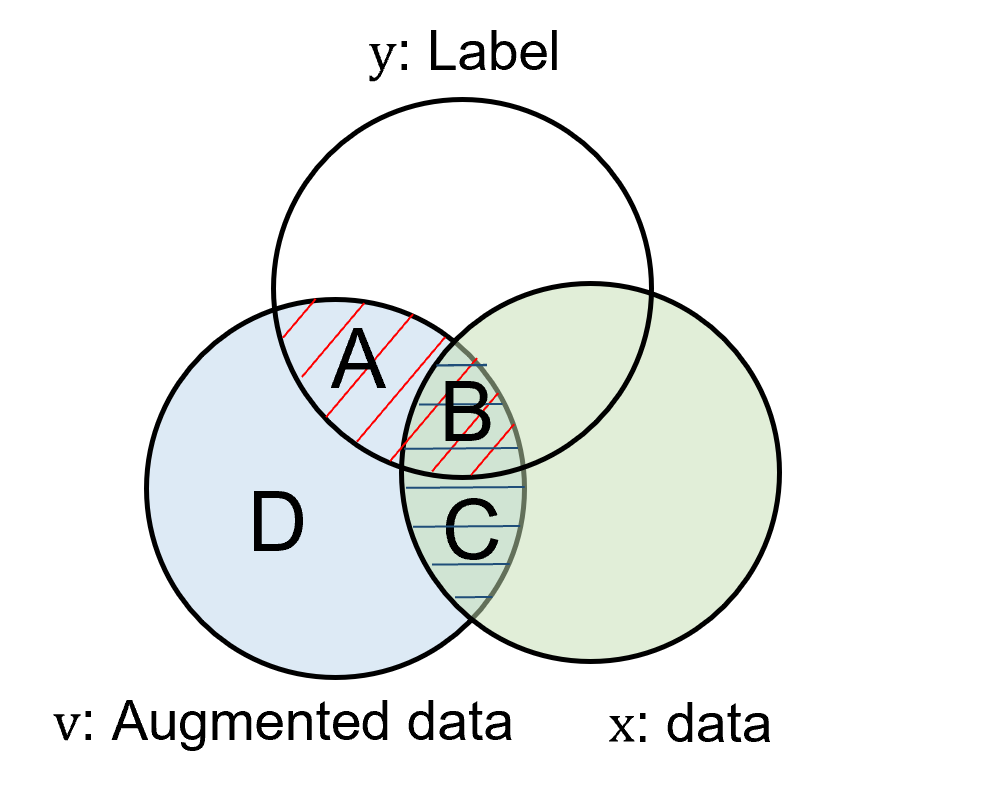
To address the challenges, we first introduce the criteria for selecting good data augmentations in contrastive learning. Data augmentation benefits generalizable, transferable, and robust representation learning by correctly extrapolating the input training space to a larger region (Wilk et al. 2018). The positive instances enclose a discriminative zone in which all the data points should be similar to the original instance. The desired data augmentations for contrastive representation learning should have both high fidelity and high variety. High fidelity encourages the augmented data to maintain the semantic identity that is invariant to transformations (Wilk et al. 2018). For example, if the downstream task is classification, then the generated augmentations of inputs should be class-preserving. Meanwhile, generating augmented samples with high variety benefits representation learning by increasing the generalization capacity (Chen et al. 2020). From the motivation, we theoretically analyze the information flows in data augmentations based on information theory and derive the criteria for selecting desired time series augmentations. Due to the inexplicability in practical time series data, we assume that the semantic identity is presented by the target in the downstream task. Thus, high fidelity can be achieved by maximizing the mutual information between the downstream label and the augmented data. A one-hot pseudo label is assigned to each instance in the unsupervised setting when downstream labels are unavailable. These pseudo-labels encourage augmentations of different instances to be distinguishable from each other. We show that data augmentations preserving these pseudo labels can add new information without decreasing the fidelity. Concurrently, we maximize the entropy of augmented data conditional on the original instances to increase the variety of data augmentations.
Based on the derived criteria, we propose an adaptive data augmentation method, InfoTS (as shown in Figure 1), to avoid ad-hoc choices or painstaking trial-and-error tuning. Specifically, we utilize another neural network, denoted by meta-learner, to learn the augmentation prior in tandem with contrastive learning. The meta-learner automatically selects optimal augmentations from candidate augmentations to generate feasible positive samples. Along with randomly sampled negative instances, augmented instances are then fed into a time series encoder to learn representations in a contrastive manner. With a reparameterization trick, the meta-learner can be efficiently optimized with back-propagation based on the proposed criteria. Therefore, the meta-learner can automatically select data augmentations in a per dataset and per learning task manner without resorting to expert knowledge or tedious downstream validation. Our main contributions include:
We propose criteria to guide the selection of data augmentations for contrastive time series representation learning without prefabricated knowledge.
We propose an approach to automatically select feasible data augmentations for different time series datasets, which can be efficiently optimized with back-propagation.
We empirically verify the effectiveness of the proposed criteria to find optimal data augmentations. Extensive experiments demonstrate that InfoTS can achieve highly competitive performance with up to 12.0% reduction in MSE on forecasting tasks and up to 3.7% relative improvement in accuracy on classification tasks over the leading baselines.
A time series instance x has dimension T × F , where T is the length of the sequence and F is the dimension of features. Given a set of time series instances X, we aim to learn an encoder fθ(x) that maps each instance x to a fixed-length vector z ∈ ℝD, where θ is the learnable parameters of the encoder network and D is the dimension of representation vectors. In semi-supervised settings, each instance x in the labeled set XL ⊆ X is associated with a label y for the downstream task. Especially, XL = X holds in the fully supervised setting. In the work, we use the Sans-serif style lowercase letters, such as x, to denote random time series variables and italic lowercase letters, such as x, for sampled instances.
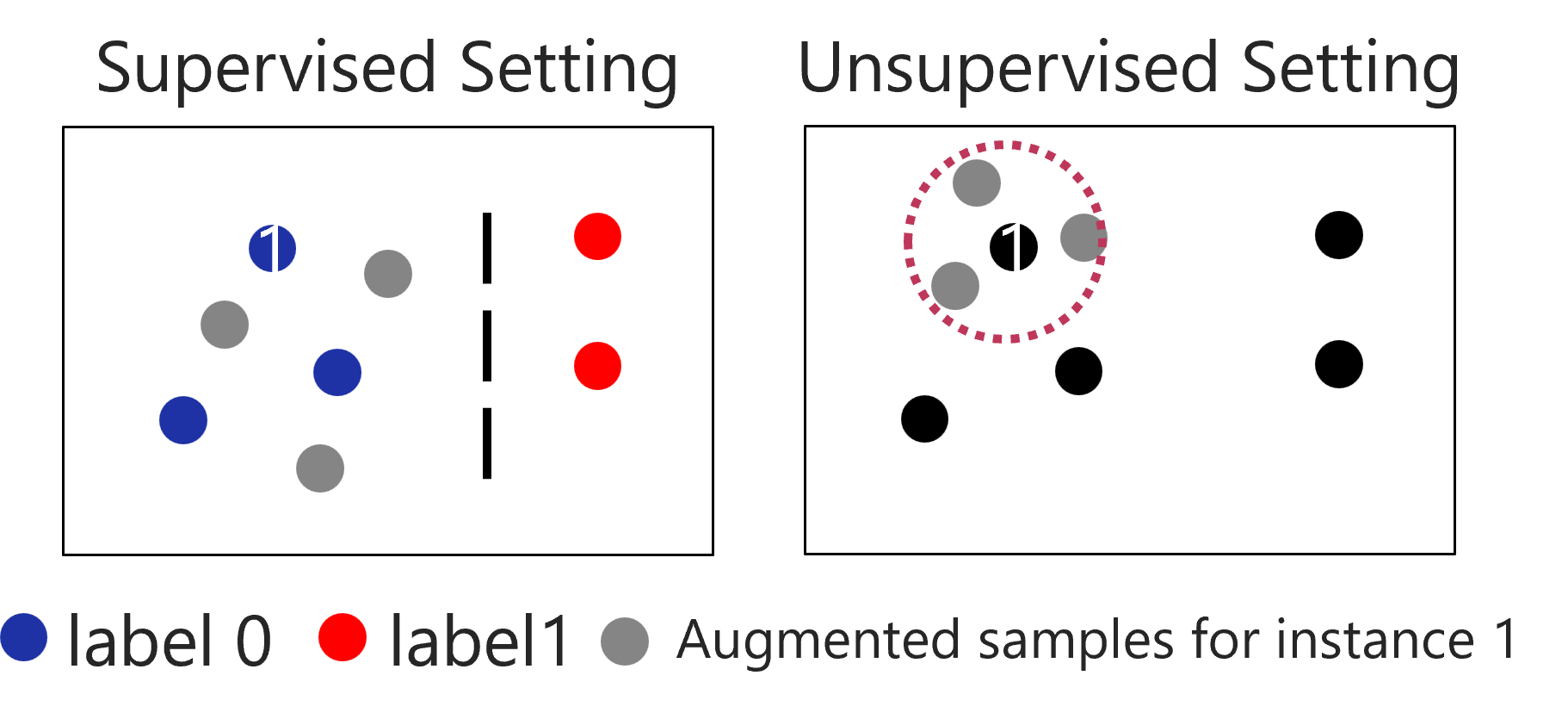
The goal of data augmentation for contrastive learning is to create realistically rational instances that maintain semantics through different transformation approaches. Unlike instances in vision and language domains, the underlying semantics of time series data is not recognizable to humans, making it hard, if not impossible, to include human knowledge to data augmentation for time series data. For example, rotating an image will not change its content or the label. While permuting a time series instance may ruin its signal patterns and generates a meaningless time series instance. In addition, the tremendous heterogeneity of real-life time series datasets further makes selections based on trial and error impractical. Although multiple data augmentation methods have been proposed for time series data, there is less discussion on what is a good augmentation that is meaningful for a given learning task and dataset without prefabricated human priors. From our perspective, ideal data augmentations for contrastive representation should keep high fidelity, high variety, and adaptive to different datasets. The illustration and examples are shown in Figure 2.
High Fidelity. Augmentations with high fidelity maintain the semantic identity that is invariant to transformations. Considering the inexplicability in practical time series data, it is challenging to visually check the fidelity of augmentations. Thus, we assume that the semantic identity of a time series instance is presented by its label in the downstream task, which might be either available or unavailable during the training period. Here, we start our analysis from the supervised case and will extend it to the unsupervised case later. Inspired by the information bottleneck (Tishby, Pereira, and Bialek 2000), we define the objective that keeps high fidelity as the large mutual information (MI) between augmentation v and the label y, i.e., MI(v;y).
We consider augmentation v as a probabilistic function of x
and a random variable ϵ, that v = g(x;ϵ). From the definition of
mutual information, we have MI(v;y) = H(y) -H(y|v), where H(y) is the (Shannon) entropy of y and H(y|v) is the entropy of
y conditioned on augmentation v. Since H(y) is irrelevant to
data augmentations, the objective is equivalent to minimizing
the conditional entropy H(y|v). Considering the efficient
optimization, we follow (Ying et al. 2019) and (Luo
et al. 2020) to approximate it with cross-entropy between y and
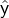, where 
is the prediction with augmentation v as the input and
calculated via
| (1) |
where z is the representation and hw(⋅) is a prediction projector parameterized by w. The prediction projector is optimized by the classification objective. Then, the objective of high fidelity for supervised or semi-supervised cases is to minimize
| (2) |
where C is the number of labels.
In the unsupervised settings where y is unavailable, one-hot encoding ys ∈ ℝ|X| is utilized as the pseudo label to replace y in Eq. (2). The motivation is that augmented instances are still distinguishable from other instances with the classifier. We theoretically show that augmentations that preserve pseudo labels have the following properties.
Property 1 (Preserving Fidelity). If augmentation v preserves the one-hot encoding pseudo label, the mutual information between v and the downstream task label y (although not visible to training) is equivalent to that between raw input x and y, i.e., MI(v;y) = MI(x;y).
Property 2 (Adding New Information). By preserving the one-hot encoding pseudo label, augmentation v contains new information comparing to the raw input x, i.e., H(v) ≥ H(x).
These properties show that in the unsupervised setting, preserving the one-hot encoding pseudo label guarantees that the generated augmentations will not decrease the fidelity, regardless of the downstream tasks and variances inherent in the augmentations. Concurrently, it may introduce new information for contrastive learning.
Since the number of labels is equal to the number of instances in dataset X in an unsupervised case, direct optimization of Eq. (2) is inefficient and unscalable. Thus, we further relax it by approximating y with the batch-wise one-hot encoding yB, which decreases the number of labels C from the dataset size to the batch size.
(a)
Information-aware
criteria |
(b)
Examples |
High Variety. Sufficient variances in augmentations improve the generalization capacity of contrastive learning models. In information theory, the uncertainty inherent in the random variable’s possible outcomes is described by its entropy. Considering that augmented instances are generated based on the raw input x, we maximize the entropy of v conditioned on x, H(v|x), to maintain a high variety of augmentations. From the definition of conditional entropy, we have
| (3) |
We dismiss the first part since the unconstrained entropy of v can be dominated by meaningless noise. Considering the continuity of both v and x, we minimize the mutual information between v and x by minimize the leave-one-out upper (L1Out) bound (Poole et al. 2019). Other MI upper bounds, such as contrastive log-ratio upper bound of mutual information (Cheng et al. 2020), can also conveniently be the plug-and-play component in our framework. Then, the objective to encourage high variety is to minimize the L1Out between v and x:
| (4) |
where v′ is an augmented instance of input instance x′. zx, zv, and zv′ are representations of instance x, v, and v′ respectively. sim(z1,z2) = z1Tz2 is the inner product of vectors z1 and z2.
Criteria. Combining the information-aware definition of both high fidelity and variety, we propose the criteria for selecting good augmentations without prior knowledge,
| (5) |
where β is a hyper-parameter to achieve the trade-off between fidelity and variety. Note that in the unsupervised settings, y is replaced by one-hot encoding pseudo label..
Relation to Information Bottleneck. Although the formation is similar to information bottleneck in data compression, minp(e|x)MI(x;e) - βMI(e;y), our criteria are different in the following aspects. First, e in the information bottleneck is a representation of input x, while v in Eq.(5) represents the augmented instances. Second, the information bottleneck aims to keep minimal and sufficient information for data compression, while our criteria are designed for data augmentations in contrastive learning. Third, in the information bottleneck, the compressed representation e is a deterministic function of input x with no variances. MI(e;y) and MI(e;x) are constraint by MI(x;y) and H(x) that MI(e;y) ≤ MI(x;y) and MI(e;x) = H(e), where H(e) is the entropy of e. In our criteria, v is a probabilistic function of input x. As a result, the variances of v make the augmentation space much larger than the compression representation space in the information bottleneck.
Relation to InfoMin. InfoMin is designed based on the information bottleneck that good views should keep minimal and sufficient information from the original input (Tian et al. 2020). Similar to the information bottleneck, InfoMin assumes that augmented views are functions of the input, which heavily constrains the variance of data augmentations. Besides, high-fidelity property is dismissed in the unsupervised setting. It works for image datasets due to the availability of human knowledge. However, it may fail to generate reasonable augmentations for time series data. In addition, they adopt adversarial learning, which minimizes a lower bound of MI, to increase the variety of augmentations. While to minimize statistical dependency, we prefer an upper bound, such as L1Out, instead of lower bounds.
We aim to design a learnable augmentation selector that learns to select feasible augmentations in a data-driven manner. With such adaptive data augmentations, the contrastive loss is then used to train the encoder that learns representations from raw time series.
The adopted encoder fθ(x) : ℝT×F → ℝD consists of two components, a fully connected layer, and a 10-layer dilated CNN module (Franceschi, Dieuleveut, and Jaggi 2019; Yue et al. 2021). To explore the inherent structure of time series, we include both global-wise (instance-level) and local-wise (subsequence-level) losses in the contrastive learning framework to train the encoder.
Global-wise contrastive loss is designed to capture the instance-level relations in a time series dataset. Formally, given a batch of time series instances XB ⊆ X, for each instance x ∈ XB, we generate an augmented instance v with an adaptively selected transformation, which will be introduced later. (x,v) is regarded as a positive pair and other (B - 1) combinations {(x,v′)}, where v′ is an augmented instance of x′ and x′≠x, are considered as negative pairs. Following (Chen et al. 2020; You et al. 2020), we design the global-wise contrastive loss based on InfoNCE (Hjelm et al. 2018). The batch-wise instance-level contrastive loss is
| (6) |
Local-wise contrastive loss is proposed to explore the
intra-temporal relations in time series. For an augmented
instance v of a time series instance x, we first split it into a set of
subsequences S, each with length L. For each subsequence
s ∈ S, we follow (Tonekaboni, Eytan, and Goldenberg 2021) to
generate a positive pair (s,p) by selecting another subsequence
close to it. Non-neighboring samples, 
s, are adopted to
generate negative pairs. Then, the local-wise contrastive loss for
an instance x is:
| (7) |
Across all instances in a batch, we have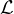 
c = 
∑
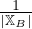x∈XB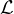cx.
The final contrastive objective is:
| (8) |
where α is a hyper-parameter to achieve the trade-off between global and local contrastive losses.
Previous time series contrastive learning methods (Franceschi, Dieuleveut, and Jaggi 2019; Fan, Zhang, and Gao 2020; Eldele et al. 2021; Tonekaboni, Eytan, and Goldenberg 2021) generate augmentations with either rule of thumb guided by prefabricated human priors or tedious trial-and-errors, which are designed for specific datasets and learning tasks. In this part, we discuss how to adaptively select the optimal augmentations with a meta-learner network based on the proposed information-aware criteria. We can regard its choice of optimal augmentation as a kind of prior selection. We first choose a set of candidate transformations T, such as jittering and time warping. Each candidate transformation ti ∈ T is associated with a weight pi ∈ (0,1), inferring the probability of selecting transformation ti. For an instance x, the augmented instance vi through transformation ti can be computed by:
| (9) |
Considering multiple transformations, we pad all vi to
be with the same length. Then, the adaptive augmented
instance can be achieved by combining candidate ones,
v =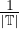 
∑
ivi.
To enable efficient optimization with gradient-based methods, we approximate discrete Bernoulli processes with binary concrete distributions (Maddison, Mnih, and Teh 2016). Specifically, we approximate ai in Eq. (9) with
| (10) |
where σ(⋅) is the sigmoid function and τ is the temperature
controlling the approximation. Moreover, with temperature
τ > 0, the gradient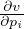 
is well-defined. Therefore, our
meta-network is end-to-end differentiable.
Contrastive learning has been utilized widely in representation learning with superior performances in various domains (Chen et al. 2020; Xie et al. 2019; You et al. 2020). Recently, some efforts have been devoted to applying contrastive learning to the time series domain (Oord, Li, and Vinyals 2018; Franceschi, Dieuleveut, and Jaggi 2019; Fan, Zhang, and Gao 2020; Eldele et al. 2021; Tonekaboni, Eytan, and Goldenberg 2021; Yue et al. 2021). Time Contrastive Learning trains a feature extractor with a multinomial logistic regression classifier to discriminate all segments in a time series (Hyvarinen and Morioka 2016). In (Franceschi, Dieuleveut, and Jaggi 2019), Franceschi et.al. generate positive and negative pairs based on subsequences. TNC employs a debiased contrastive objective to ensure that in the representation space, signals in the local neighborhood are distinguishable from non-neighboring signals (Tonekaboni, Eytan, and Goldenberg 2021). SelfTime adopts multiple hand-crafted augmentations for unsupervised time series contrastive learning by exploring both inter-sample and intra-sample relations (Fan, Zhang, and Gao 2020). TS2Vec learns a representation for each time stamp and conducts contrastive learning in a hierarchical way (Yue et al. 2021). However, data augmentations in these methods are either universal or selected by error and trail, hindering them away from being widely applied in complex real-life datasets.
Forecasting is a critical task in time series analysis. Deep learning architectures used in the literature include Recurrent Neural Networks (RNNs) (Salinas et al. 2020; Oreshkin et al. 2019), Convolutional Neural Networks (CNNs) (Bai, Kolter, and Koltun 2018), Transformers (Li et al. 2019; Zhou et al. 2021), and Graph Neural Networks (GNNs) (Cao et al. 2021). N-BEATS deeply stacks fully-connected layers with backward and forward residual links for univariate times series forecasting (Oreshkin et al. 2019). TCN utilizes a deep CNN architecture with dilated causal convolutions (Bai, Kolter, and Koltun 2018). Considering both long-term dependencies and short-term trends in multivariate time series, LSTnet combines both CNNs and RNNS in a unified model (Lai et al. 2018). LogTrans brings the Transformer model to time series forecasting with causal convolution in its attention mechanism (Li et al. 2019). Informer further proposes a sparse self-attention mechanism to reduce the time complexity and memory usage (Zhou et al. 2021). StemGNN is a GNN-based model that considers the intra-temporal and inter-series correlations simultaneously (Cao et al. 2021). Unlike these works, we aim to learn general representations for time series data that can not only be used for forecasting but also for other tasks, such as classification. Besides, the proposed framework is compatible with various architectures as encoders.
Data augmentation is an important component of contrastive learning. Existing researches reveal that the choices of optimal augmentation are dependent on downstream tasks and datasets (Chen et al. 2020; Fan, Zhang, and Gao 2020). Some researchers have explored adaptive selections of optimal augmentations for contrastive learning in the visual field. AutoAugment automatically searches the combination of translation policies via a reinforcement learning method (Cubuk et al. 2019). Faster-AA improves the searching pipeline for data augmentation using a differentiable policy network (Hataya et al. 2020). DADA further introduces an unbiased gradient estimator for an efficient one-pass optimization strategy (Li et al. 2020). Within contrastive learning frameworks, Tian et.al. apply the Information Bottleneck theory that optimal views should share minimal and sufficient information, to guide the selection of good views for contrastive learning in the vision domain (Tian et al. 2020). Considering the inexplicability of time series data, directly applying the InfoMin framework may keep insufficient information during augmentation. Different from (Tian et al. 2020), we focus on the time series domain and propose an end-to-end differentiable method to automatically select the optimal augmentations for each dataset.
In this section, we compare InfoTS with SOTA baselines on time series forecasting and classification tasks. We also conduct case studies to show insights into the proposed criteria and meta-learner network. Detailed experimental setups are shown in Appendix. Full experimental results and extra experiments are presented in Appendix.
| InfoTS | TS2Vec | Informer | LogTrans | N-BEATS | TCN | LSTnet
| |||||||||
| Dataset | Ly | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE |
|
ETTh1 | 24 | 0.039 | 0.149 | 0.039 | 0.152 | 0.098 | 0.247 | 0.103 | 0.259 | 0.094 | 0.238 | 0.075 | 0.210 | 0.108 | 0.284 |
| 48 | 0.056 | 0.179 | 0.062 | 0.191 | 0.158 | 0.319 | 0.167 | 0.328 | 0.210 | 0.367 | 0.227 | 0.402 | 0.175 | 0.424 | |
| 168 | 0.100 | 0.239 | 0.134 | 0.282 | 0.183 | 0.346 | 0.207 | 0.375 | 0.232 | 0.391 | 0.316 | 0.493 | 0.396 | 0.504 | |
| 336 | 0.117 | 0.264 | 0.154 | 0.310 | 0.222 | 0.387 | 0.230 | 0.398 | 0.232 | 0.388 | 0.306 | 0.495 | 0.468 | 0.593 | |
| 720 | 0.141 | 0.302 | 0.163 | 0.327 | 0.269 | 0.435 | 0.273 | 0.463 | 0.322 | 0.490 | 0.390 | 0.557 | 0.659 | 0.766 | |
|
ETTh2 | 24 | 0.081 | 0.215 | 0.090 | 0.229 | 0.093 | 0.240 | 0.102 | 0.255 | 0.198 | 0.345 | 0.103 | 0.249 | 3.554 | 0.445 |
| 48 | 0.115 | 0.261 | 0.124 | 0.273 | 0.155 | 0.314 | 0.169 | 0.348 | 0.234 | 0.386 | 0.142 | 0.290 | 3.190 | 0.474 | |
| 168 | 0.171 | 0.327 | 0.208 | 0.360 | 0.232 | 0.389 | 0.246 | 0.422 | 0.331 | 0.453 | 0.227 | 0.376 | 2.800 | 0.595 | |
| 336 | 0.183 | 0.341 | 0.213 | 0.369 | 0.263 | 0.417 | 0.267 | 0.437 | 0.431 | 0.508 | 0.296 | 0.430 | 2.753 | 0.738 | |
| 720 | 0.194 | 0.357 | 0.214 | 0.374 | 0.277 | 0.431 | 0.303 | 0.493 | 0.437 | 0.517 | 0.325 | 0.463 | 2.878 | 1.044 | |
|
ETTm1 | 24 | 0.014 | 0.087 | 0.015 | 0.092 | 0.030 | 0.137 | 0.065 | 0.202 | 0.054 | 0.184 | 0.041 | 0.157 | 0.090 | 0.206 |
| 48 | 0.025 | 0.117 | 0.027 | 0.126 | 0.069 | 0.203 | 0.078 | 0.220 | 0.190 | 0.361 | 0.101 | 0.257 | 0.179 | 0.306 | |
| 96 | 0.036 | 0.142 | 0.044 | 0.161 | 0.194 | 0.372 | 0.199 | 0.386 | 0.183 | 0.353 | 0.142 | 0.311 | 0.272 | 0.399 | |
| 288 | 0.071 | 0.200 | 0.103 | 0.246 | 0.401 | 0.554 | 0.411 | 0.572 | 0.186 | 0.362 | 0.318 | 0.472 | 0.462 | 0.558 | |
| 672 | 0.102 | 0.240 | 0.156 | 0.307 | 0.512 | 0.644 | 0.598 | 0.702 | 0.197 | 0.368 | 0.397 | 0.547 | 0.639 | 0.697 | |
|
Electricity | 24 | 0.245 | 0.269 | 0.260 | 0.288 | 0.251 | 0.275 | 0.528 | 0.447 | 0.427 | 0.330 | 0.263 | 0.279 | 0.281 | 0.287 |
| 48 | 0.294 | 0.301 | 0.319 | 0.324 | 0.346 | 0.339 | 0.409 | 0.414 | 0.551 | 0.392 | 0.373 | 0.344 | 0.381 | 0.366 | |
| 168 | 0.402 | 0.367 | 0.427 | 0.394 | 0.544 | 0.424 | 0.959 | 0.612 | 0.893 | 0.538 | 0.609 | 0.462 | 0.599 | 0.500 | |
| 336 | 0.533 | 0.453 | 0.565 | 0.474 | 0.713 | 0.512 | 1.079 | 0.639 | 1.035 | 0.669 | 0.855 | 0.606 | 0.823 | 0.624 | |
| Avg. | 0.154 | 0.253 | 0.175 | 0.278 | 0.263 | 0.367 | 0.336 | 0.419 | 0.338 | 0.402 | 0.289 | 0.359 | 1.090 | 0.516 | |
| Method | InfoTSs | InfoTS | TS2Vec | T-Loss | TNC | TS-TCC | TST | DTW |
| Avg. ACC | 0.730 | 0.714 | 0.704 | 0.658 | 0.670 | 0.668 | 0.617 | 0.629 |
| Avg. Rank | 1.967 | 2.633 | 3.067 | 3.833 | 4.367 | 4.167 | 5.0 | 4.366 |
Time series forecasting aims to predict the future Ly time stamps, with the last Lx observations. We follow (Yue et al. 2021) to train a linear model regularized with the L2 norm penalty to make predictions. The output has dimension Ly in the univariate case and Ly ×F for the multivariate case, where F is the feature dimension.
Datasets and Baselines. Four benchmark datasets for time series forecasting are adopted, including ETTh1, ETTh2, ETTm1 (Zhou et al. 2021), and the Electricity dataset (Dua and Graff 2017). These datasets are used in both univariate and multivariate settings. We compare unsupervised InfoTS to the SOTA baselines, including TS2Vec (Yue et al. 2021), Informer (Zhou et al. 2021), StemGNN (Cao et al. 2021), TCN (Bai, Kolter, and Koltun 2018), LogTrans (Li et al. 2019), LSTnet (Lai et al. 2018), and N-BEATS (Oreshkin et al. 2019). Among these methods, N-BEATS is merely designed for the univariate and StemGNN is for multivariate only. We refer to (Yue et al. 2021) to set up baselines for a fair comparison. Standard metrics for a regression problem, Mean Squared Error (MSE), and Mean Absolute Error (MAE) are utilized for evaluation. Evaluation results of univariate time series forecasting are shown in Table 1.
Performance. As shown in Tabel 1 and Tabel ??, comparison in both univariate and multivariate settings indicates that InfoTS consistently matches or outperforms the leading baselines. Some results of StemGNN are unavailable due to the out-of-memory issue (Yue et al. 2021). Specifically, we have the following observations. TS2Vec, another contrastive learning method with data augmentations, achieves the second-best performance in most cases. The consistent improvement of TS2Vec over other baselines indicates the effectiveness of contrastive learning for time series representations learning. However, such universal data augmentations may not be the most informative ones to generate positive pairs. Compared to TS2Vec, InfoTS decreases the average MSE by 12.0%, and the average MAE by 9.0% in the univariate setting. In the multivariate setting, the MSE and MAE decrease by 5.5% and 2.3%, respectively. The reason is that InfoTS can adaptively select the most suitable augmentations in a data-driven manner with high variety and high fidelity. Encoders trained with such informative augmentations learn representations with higher quality.
Following the previous setting, we evaluate the quality of representations on time series classification in a standard supervised manner (Franceschi, Dieuleveut, and Jaggi 2019; Yue et al. 2021). We train an SVM classifier with a radial basis function kernel on top of representations in the training split and then compare the prediction in the test set.
Datasets and Baselines. The UEA archive (Bredin 2017) consists of 30 multivariate datasets. We compare InfoTS with baselines including TS2Vec (Yue et al. 2021), T-Loss (Franceschi, Dieuleveut, and Jaggi 2019), TS-TCC (Eldele et al. 2021), TST (Zerveas et al. 2021), and DTW (Franceschi, Dieuleveut, and Jaggi 2019). For our methods, InfoTSs, training labels are only used to train the meta-learner network to select suitable augmentations, and InfoTS is with a purely unsupervised setting for representation learning.
Performance. The results on the UEA datasets are summarized in Table 2. With the ground-truth label guiding the meta-learner network, InfoTSs substantially outperforms other baselines. On average, it improves the classification accuracy by 3.7% over the best baseline, TS2Vec, with an average rank value of 1.967 on all 30 UEA datasets. Under the purely unsupervised setting, InfoTS preserves fidelity by adopting one-hot encoding as the pseudo labels. InfoTS achieves the second-best average performance in Table 2, with an average rank value of 2.633.
To present deep insights into the proposed method, we conduct multiple ablation studies on the Electricity dataset to empirically verify the effectiveness of the proposed information aware criteria and the framework to adaptively select suitable augmentations. MSE is utilized for evaluation.
|
InfoTS | Data Augmentation | Meta Objective
| |||
| Random | All | w/o Fidelity | w/o Variety | ||
| 24 | 0.245 | 0.252 | 0.249 | 0.254 | 0.251 |
| 48 | 0.294 | 0.303 | 0.303 | 0.306 | 0.297 |
| 168 | 0.402 | 0.414 | 0.414 | 0.414 | 0.409 |
| 336 | 0.533 | 0.565 | 0.563 | 0.562 | 0.542 |
| Avg. | 0.369 | 0.384 | 0.382 | 0.384 | 0.375 |
Evaluation of The Criteria. We propose information-aware criteria of data augmentations for time series that good augmentations should have high variety and fidelity. With L1Out and cross-entropy as approximations, we get the criteria in Eq. (5). To empirically verify the effectiveness of the proposed criteria, we adopt two groups of augmentations, subsequence augmentations with different lengths and jitter augmentations with different standard deviations. Subsequence augmentations work on the temporal dimension, and jitter augmentations work on the feature dimension. For the subsequence augmentations, we range the ratio of subsequences r in the range [0.01,0.99]. The subsequence augmentation with ratio r is denoted by Subr, such as Sub0.01. For the jitter augmentations, the standard deviations are chosen from the range [0.01,3.0]. The jitter augmentation with standard deviation std is denoted by Jitterstd, such as Jitter0.01.
Intuitively, with r increasing, Subr generates augmented instances with lower variety and higher fidelity. For example, with r = 0.01, Subr generates subsequences that only keep 1% time stamps from the original input, leading to high variety but extremely low fidelity. Similarly, for jitter augmentations, with std increasing, Jitterstd generates augmented instances with higher variety but lower fidelity.
In Figure 3, we show the relationship between forecasting performance and our proposed criteria. In general, performance is positively related to the proposed criteria in both MAE and MSE settings, verifying the correctness of using the criteria as the objective in the meta-learner network training.
Evaluation of The Meta-Learner Network. In this part, we empirically show the advantage of the developed meta-learner network on learning optimal augmentations. Results are shown in Table 3. We compare InfoTS with variants “Random” and “All”. “Random” randomly selects an augmentation from candidate transformation functions each time and “All” sequentially applies transformations to generate augmented instances. Their performances are heavily affected by low-quality candidate augmentations, verifying the key role of adaptive selection in our method. 2) To show the effects of variety and fidelity objectives in meta-learner network training, we include two variants, “w/o Fidelity” and “w/o Variety”, which dismiss the fidelity or variety objective, respectively. The comparison between InfoTS and the variants empirically confirms both variety and fidelity are important for data augmentation in contrastive learning.
We propose information-aware criteria of data augmentations for time series data that good augmentations should preserve high variety and high fidelity. We approximate the criteria with a mutual information neural estimation and cross-entropy estimation. Based on the approximated criteria, we adopt a meta-learner network to adaptively select optimal augmentations for contrastive representation learning. Comprehensive experiments show that representations produced by our method are highly qualified and easy to use in various downstream tasks, such as time series forecasting and classification, with state-of-the-art performances.
This project was partially supported by NSF grant IIS-1707548.
Bai, S.; Kolter, J. Z.; and Koltun, V. 2018. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv preprint arXiv:1803.01271.
Bredin, H. 2017. Tristounet: triplet loss for speaker turn embedding. In ICASSP, 5430–5434.
Cao, D.; Wang, Y.; Duan, J.; Zhang, C.; Zhu, X.; Huang, C.; Tong, Y.; Xu, B.; Bai, J.; Tong, J.; et al. 2021. Spectral temporal graph neural network for multivariate time-series forecasting. arXiv preprint arXiv:2103.07719.
Chen, T.; Kornblith, S.; Norouzi, M.; and Hinton, G. 2020. A simple framework for contrastive learning of visual representations. In ICML, 1597–1607.
Cheng, P.; Hao, W.; Dai, S.; Liu, J.; Gan, Z.; and Carin, L. 2020. Club: A contrastive log-ratio upper bound of mutual information. In International Conference on Machine Learning, 1779–1788. PMLR.
Cubuk, E. D.; Zoph, B.; Mane, D.; Vasudevan, V.; and Le, Q. V. 2019. Autoaugment: Learning augmentation strategies from data. In CVPR, 113–123.
Dua, D.; and Graff, C. 2017. UCI Machine Learning Repository.
Eldele, E.; Ragab, M.; Chen, Z.; Wu, M.; Kwoh, C. K.; Li, X.; and Guan, C. 2021. Time-Series Representation Learning via Temporal and Contextual Contrasting. arXiv preprint arXiv:2106.14112.
Fan, H.; Zhang, F.; and Gao, Y. 2020. Self-Supervised Time Series Representation Learning by Inter-Intra Relational Reasoning. arXiv preprint arXiv:2011.13548.
Franceschi, J.-Y.; Dieuleveut, A.; and Jaggi, M. 2019. Unsupervised scalable representation learning for multivariate time series. arXiv preprint arXiv:1901.10738.
Hataya, R.; Zdenek, J.; Yoshizoe, K.; and Nakayama, H. 2020. Faster autoaugment: Learning augmentation strategies using backpropagation. In ECCV, 1–16. Springer.
Hjelm, R. D.; Fedorov, A.; Lavoie-Marchildon, S.; Grewal, K.; Bachman, P.; Trischler, A.; and Bengio, Y. 2018. Learning deep representations by mutual information estimation and maximization. arXiv preprint arXiv:1808.06670.
Hyvarinen, A.; and Morioka, H. 2016. Unsupervised feature extraction by time-contrastive learning and nonlinear ica. In NIPS, 3765–3773.
Lai, G.; Chang, W.-C.; Yang, Y.; and Liu, H. 2018. Modeling long-and short-term temporal patterns with deep neural networks. In SIGIR, 95–104.
Li, S.; Jin, X.; Xuan, Y.; Zhou, X.; Chen, W.; Wang, Y.-X.; and Yan, X. 2019. Enhancing the locality and breaking the memory bottleneck of transformer on time series forecasting. In NeurIPS, 5243–5253.
Li, Y.; Hu, G.; Wang, Y.; Hospedales, T.; Robertson, N. M.; and Yang, Y. 2020. DADA: Differentiable automatic data augmentation. arXiv preprint arXiv:2003.03780.
Luo, D.; Cheng, W.; Ni, J.; Yu, W.; Zhang, X.; Zong, B.; Liu, Y.; Chen, Z.; Song, D.; Chen, H.; et al. 2021. Unsupervised Document Embedding via Contrastive Augmentation. arXiv preprint arXiv:2103.14542.
Luo, D.; Cheng, W.; Xu, D.; Yu, W.; Zong, B.; Chen, H.; and Zhang, X. 2020. Parameterized explainer for graph neural network. arXiv preprint arXiv:2011.04573.
Maddison, C. J.; Mnih, A.; and Teh, Y. W. 2016. The concrete distribution: A continuous relaxation of discrete random variables. arXiv preprint arXiv:1611.00712.
Oord, A. v. d.; Li, Y.; and Vinyals, O. 2018. Representation learning with contrastive predictive coding. arXiv preprint arXiv:1807.03748.
Oreshkin, B. N.; Carpov, D.; Chapados, N.; and Bengio, Y. 2019. N-BEATS: Neural basis expansion analysis for interpretable time series forecasting. arXiv preprint arXiv:1905.10437.
Poole, B.; Ozair, S.; Van Den Oord, A.; Alemi, A.; and Tucker, G. 2019. On variational bounds of mutual information. In International Conference on Machine Learning, 5171–5180. PMLR.
Salinas, D.; Flunkert, V.; Gasthaus, J.; and Januschowski, T. 2020. DeepAR: Probabilistic forecasting with autoregressive recurrent networks. International Journal of Forecasting, 36(3): 1181–1191.
Tian, Y.; Sun, C.; Poole, B.; Krishnan, D.; Schmid, C.; and Isola, P. 2020. What makes for good views for contrastive learning? arXiv preprint arXiv:2005.10243.
Tishby, N.; Pereira, F. C.; and Bialek, W. 2000. The information bottleneck method. arXiv preprint physics/0004057.
Tonekaboni, S.; Eytan, D.; and Goldenberg, A. 2021. Unsupervised representation learning for time series with temporal neighborhood coding. arXiv preprint arXiv:2106.00750.
Wen, Q.; Sun, L.; Song, X.; Gao, J.; Wang, X.; and Xu, H. 2021. Time Series Data Augmentation for Deep Learning: A Survey. In AAAI.
Wilk, M. v. d.; Bauer, M.; John, S.; and Hensman, J. 2018. Learning invariances using the marginal likelihood. In NeurIPS, 9960–9970.
Xie, Q.; Dai, Z.; Hovy, E.; Luong, M.-T.; and Le, Q. V. 2019. Unsupervised data augmentation for consistency training. arXiv preprint arXiv:1904.12848.
Yang, Q.; and Wu, X. 2006. 10 challenging problems in data mining research. International Journal of Information Technology & Decision Making, 5(04): 597–604.
Ying, R.; Bourgeois, D.; You, J.; Zitnik, M.; and Leskovec, J. 2019. Gnnexplainer: Generating explanations for graph neural networks. In NeurIPS, volume 32, 9240.
You, Y.; Chen, T.; Sui, Y.; Chen, T.; Wang, Z.; and Shen, Y. 2020. Graph contrastive learning with augmentations. In NeurIPS, 5812–5823.
Yue, Z.; Wang, Y.; Duan, J.; Yang, T.; Huang, C.; and Xu, B. 2021. TS2Vec: Towards Universal Representation of Time Series. arXiv preprint arXiv:2106.10466.
Zerveas, G.; Jayaraman, S.; Patel, D.; Bhamidipaty, A.; and Eickhoff, C. 2021. A transformer-based framework for multivariate time series representation learning. In SIGKDD, 2114–2124.
Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; and Zhang, W. 2021. Informer: Beyond efficient transformer for long sequence time-series forecasting. In AAAI.
![[ ]
------exp(sim-(zx,zv))-----
IL1Out(v;x) = Ex log∑x ′∈X,x′⁄=xexp(sim (zx,zv′)) ,](main5x.png)
