Notes Taker: Congjun Yang
Lecture # 17
Date : Nov 9th ’98.

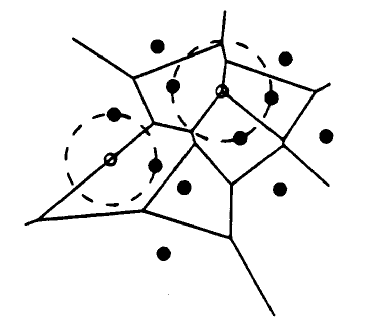
Voronoi Diagram

1. DEFINITION

Let P = {p₁, p₂, …, p_n} be a set of n given point sites in the plane. We define the Voronoi diagram of P as the subdivision of the plane into n cells, one for each site in P, with the property that a point q lies in the cell corresponding to a cell p_iiff dist(q, p_i) < dist(q, p_j) for each p_j in P with j ¹ i. We denote the Voronoi diagram of P by Vor(P). The cell that corresponds to a site p_i is denoted V(p_i).

The Voronoi diagram is a planar subdivision whose edges are straight line segments. Some edges are line segments and others are half-lines. Unless all sites are collinear there will be no edges that are full lines.

2. PROPERTIES OF THE VORONOI DIAGRAM

THEOREM 1: The Voronoi diagram of a set of n point sites in the plane has at most 2n-5 vertices and 3n-6 edges.

Idea of Proof: Using Euler's formula: for any connected planar embedded graph with n_vnodes, n_e edges, and n_f faces the relation n_v - n_e + n_f = 2 holds.

We know that edges of Vor(P) are parts of bisectors of pairs of sites and the vertices of Vor(P) are intersection points between these bisectors. There is a quadratic number of bisectors, whereas the complexity of the Vor(P) is linear. Hence, not all bisectors define edges of Vor(P) and not all intersections are vertices of Vor(P). The following theorem characterizes the vertices and edges of the Voronoi diagram.

THEOREM 2: For the Voronoi diagram Vor(S) of a set of points S the following holds:

A point q is a vertex of Vor(S) iff its largest empty circle C(q) contains three or more sites on its boundary.
The bisector between sites p_i and p_j defines an edge of Vor(S) iff there is a point q in R² such that C(q) contains both p_i and p_j on its boundary but no other site.

In the theorem, the largest empty circle of a point q, denoted C(q), is defined as the largest circle with q as its center that does not contain any site of P in its interior.

3. COMPUTING THE VORONOI DIAGRAM (Fortune's Algorithm)

Strategy: Sweep a horizontal line - the sweep line - from top to bottom over the plane.

Difficulty:The part of Vor(P) above the sweep line l depends not only on the sites above l but also on sites below l.

Observation:For any point q above the sweep line l, the nearest site of q cannot lie below l if q is at least as near to some site above l as q is to l.

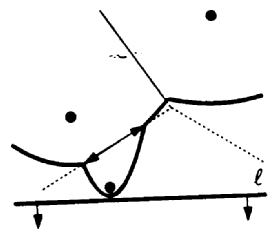
Beach line: The locus of the points that are closer to some site above the line l than to l itself is bounded by parabolic arcs. We call the sequence of parabolic arcs the beach line. This is shown by the thick piecewise smooth curve in the figure below.

Inductive Assumption: By the observation above, we inductively assume that Vor(P) is completely determined above the beach line. The portion between the beach line and the sweep line cannot yet be determined since it could be affected by points below the sweep line l that have not yet been encountered.

It is easy to see that several disjoint portions of the same parabola can be part of the beach line. Notice that the breakpoints between the different parabolic arcs forming the beach line lie on edges of the Voronoi diagram. The breakpoints exactly trace out the Voronoi diagram as the sweep line moves from top to bottom.

We do not maintain the beach line explicitly, since it changes continuously as l moves. Instead, we only maintain the breakpoints using a binary tree T as follows.

Each leaf stores the site that defines the arc it represents. The internal nodes represent the breakpoints on the beach line. A breakpoint is stored at an internal node by an ordered pair of sites <p_i, p_j>, where pi defines the parabola left of the breakpoint and p_j defines the parabola to the right.

When and how does the combinatorial structure of the beach line change? This happens either when a new parabolic arc appears on it or when a parabolic arc shrinks to a point and disappears.

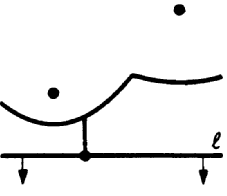
Site Event: When the sweep line reaches a new site, a new arc will appear first as a degenerate parabola. As the sweep line moves down the new parabola gets wider and wider. At a site event two new breakpoints appear and start tracing out edges.

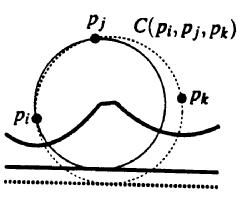
Circle Event: For any three consecutive arcs a, a’, and a" defined by three distinct sites p_i, p_j, and p_k, at the moment an arc a’ disappears, the parabolas defined by these three sites pass through a common point q. Point q is equidistant from l and each of the three sites. There is a circle passing through p_i, p_j, and p_kwith q as its center whose lowest point lies on l. There cannot be a site in the interior of this circle: such a site would be closer to q than q is to l, contradicting the fact that q is on the beach line. It follows that q is a vertex of the Voronoi diagram.

So when an arc disappears from the beach line and two break points meet, two edges meet as well. We call the event where the sweep line reaches the lowest point of a circle through three sites defining consecutive arcs on the beach line a circle event.

The event queue Q is implemented as a priority queue, where the priority of an event is its y-coordinate. It stores the upcoming events.

All site events are known in advance.
Detection of the circle events: For any three consecutive arcs on the beach line, the corresponding circle event is in the event queue Q if the circle intersects the sweep line. If the circle lies completely above the sweep line, then the event has already been dealt with. Also if the circle contains some other sites in its interior the event should not be handled.

When a triple of consecutive arcs is destroyed, we delete the corresponding circle event from Q, if it occurs in Q. Suppose that an arc disappears from the beach line, or it is split, and we wish to delete all circle events the arc participates in. We first search in T for the leaf m storing the site defining the arc. At that leaf there is a pointer to a circle event to let us find the circle event in the event queue Q quickly.

Now, we are at the point to see the exact algorithm

Algorithm VoronoiDiagram(P)

Input: A set P = {p₁, p₂, … , p_n} of point sites in the plane.
Output: The Voronoi diagram Vor(P) given inside a bounding box in a doubly-connected edge list structure.

Initialize the event queue Q with all site events.
While Q is not empty Do
Consider the event with largest y -coordinate in Q.
If the event is a site event, occurring at site p_i
Then HandleSiteEvent(p_i)
Else HandleCircleEvent(p_l), where p_l is the lowest point of the circle causing the event.
Remove the event from Q.
The internal nodes still present in T correspond to the half-infinite edges of the Voronoi diagram. Compute a bounding box that contains all vertices of the Voronoi diagram in its interior, and attach the half-infinite edges to the bounding box by updating the doubly connected edge list appropriately.
Traverse the half-edges of the doubly connected edge list to add the cell records and the pointers to and from them.

The procedures to handle the events are defined as follows.

HandleSiteEvent(p_I)

Search in T for the arc a vertically above p_i, and delete all circle events involving a from Q.
Replace the leaf of T that represents a with a subtree having three leaves. The middle leaf stores the new site p_i and the other two leaves store the site p_j that was originally stored with a. Store the tuple <p_j, p_i> and <p_i, p_j> representing the new breakpoints at the two new internal nodes. Perform re-balancing operations on T if necessary.
Create new records in the Voronoi diagram structure for the two half-edges separating V(p_i) and V(p_j), which will be traced out by the two new breakpoints.
Check the triples of consecutive arcs involving one of the three new arcs. Insert the corresponding circle event only if the circle intersects the sweep line and the circle event is not present yet in Q.

HandleCircleEvent(p_l)

Search in T for the arc a vertically above p_l that is about to disappear, and delete all circle events that involve a from Q.
Delete the leaf that represents a from T. Update the tuples representing the breakpoints at the internal nodes. Perform re-balancing operations on T if necessary.
Add the center of the circle causing the event as a vertex record in the Voronoi diagram structure and create two half-edge records corresponding to the new breakpoint of the Voronoi diagram. Set the pointers between them appropriately.
Check the new triples of consecutive arcs that arise because of the disappearance of a. Insert the corresponding circle event into Q only if the circle intersects the sweep line and the circle event isn’t present yet in Q.

Finally, let’s see the complexity of Fortune’s algorithm. In particular, we have the following theorem.

THEOREM 3: The algorithm runs in O(n log n) time and it uses O(n) storage.

Proof: The primitive operations on the tree T and the event queue Q, such as inserting or deleting an element, take O(log n) time each. The primitive operations on the data structure containing the Voronoi diagram, i.e., the doubly connected edge list, take constant time. To handle an event we do a constant number of such primitive operations, so we spend O(log n) time to process an event. Obviously, there are n site events. As for the number of circle events, we observe that every such event that is processed defines a vertex of Vor(P). Note that false alarms (the circle events that do not define a vertex) are deleted before they are processed. They are processed and deleted while processing another real event and the time we spend on them is subsumed under the time we spend to process this event. Hence, the number of circle events that we process is at most 2n – 5. The time and storage bounds follow.