A polynomial time algorithm finds a solution to a problem, in time polynomial in the size of the input length.

There is a large class of important problems known as the NP-complete problems. It is believed that no polynomial time algorithms exist for solving NP-complete problems.

To deal with NP-complete problems, there are some possible ways. One way is to find near-optimal solutions in polynomial time (either in the worst case or on the average). In practice, near-optimality is often good enough. An algorithm that returns near-optimal solutions is called an approximation algorithm. Instead of finding the optimal solution, we can find a "good" solution for the problem.

An approximation algorithm is not simply to find a good solution, but the value of the solution found must be bound relative to the value of an optimal solution.

We say that an approximation algorithm for the problem has a ratio bound of p(n) if for any input of size n, the cost C of the solution produced by the approximation algorithm is within a factor of p(n) of the cost C* of an optimal solution:

max (C/C*, C*/C) £ p(n)

This definition applies for both minimization and maximization problems. The ratio bound of an approximation algorithm is never less than 1, and an approximation algorithm with a large ratio bound may return a solution that is much worse than the optimal.

A vertex cover of a graph is defined as a set of vertices that are incident on all the edges of the graph. The vertex-cover problem is to find a vertex cover of minimum size in a give undirected graph. This problem is NP-hard. It is difficult to find an optimal vertex cover in a graph G, however, it is not too hard to find a vertex cover that is near-optimal.

We start with a simple idea: a greedy algorithm. Examine the edges of the graph in arbitrary order then

• Add both endpoint to the vertex cover
• Discard all edges covered by either vertex

Approx-Vertex-Cover(G)

1. C ¬ 0
2. E’ ¬ E[G]
3. while E’ ¹ 0
4. do let (u, v) be an arbitrary edge of E’
5. C ¬ C È {(u, v)}
6. remove from E’ every edge incident on either u or v
7. return C

Approx-Vertex-Cover has a ratio bound of 2

The set C of vertices that is returned by Approx-Vertex-Cover is a vertex cover, since the algorithm loops until every edge in E[G] has been covered by some vertex in C.

To see that Approx-Vertex-Cover returns a vertex cover that is at most twice the size of an optimal cover, let A denote the set of edges that were picked in line 4 of Approx-Vertex-Cover. No two edges in A share en endpoint, since once an edge is picked in line 4, all other edges that are incident on its endpoints are deleted from E’ in line 6. Therefore, each execution of line 5 adds two new vertices to C, and |C| = 2|A|. In order to cover the edges in A, however, any vertex cover - in particular, an optimal cover C* - must include at least one endpoint of each edge in A. Since no two edges in A share an endpoint, no vertex in the cover is incident on more than one edge in A. Therefore, |A| £ |C*|, and |C| £ 2|C*|.

This algorithm is the best known approximation algorithm for the minimum vertex cover problem.

In the traveling salesperson problem, we are given a complete undirected graph G = (V, E) that has weight function w(u, v) associated with each edge (u, v) Î E, and we must find a tour of G with minimum weight.

In many practical situation, it is always cheapest to go directly from a place u to a place q; going by way of any intermediate stop v can’t be less expensive. The triangle inequality is that for all vertices u, v, q Î V,

w(u, q) £ w(u, v) + w(v, q)

This means that, cutting out an intermediate stop never increases the weight. In many applications it is automatically satisfied.

Approx-TSP-Tour(G, w)

1. Find a minimum spanning tree T for the given set of city
1. Double the MST and construct a tour T’
1. Add shortcut so that no city is visited more than once and output the resulting tour T

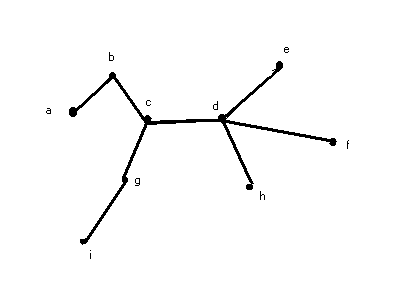
Below is a example:

Step 1: We have a MST for 9 cities

Step 2: By doubling the MST, we construct the tour T’ = a - b - c - d - e - d - f - d - h - d –

c - g - i - g - c - b - a

This tour visit some cities more than once. Here is where the triangle inequality helps us. We can avoid repeated cities by introducing "shortcuts" that do not increase the total length of the traversal.

Step 3: After add shortcuts, we obtain the tour T = a - b - c - d - e - f - h - g - i - a

Approx-TSP-Tour is an approximation algorithm with a ratio bound of 2 for the traveling salesman problem with triangle inequality.

If the length of MST is |MST|, then after step 2, |T’| = 2 |MST| because T’ double the MST. At the step 3, we add shortcuts, so |T |£ |T’| by using triangle inequality. Therefore, |T| £ 2 |MST|.

Now, we need to prove that |MST| £ |T_opt|.

We can observe that deleting any edge from a optimal tour T_opt yields a spanning tree consisting of a single path through all the cities. Thus the optimal traveling salesman tour T_opt must be strictly longer than the minimum spanning tree |MST|.

Combining inequalities |T| £ 2 |MST| and |MST| £ |T_opt|, we got |T| £ 2 |T_opt|.

In spite of the nice ratio bound provided by this theorem, Approx-TSP-Tour has been improved. Christofides’ algorithm for the TSP with the triangle inequality has a ratio bound of 3/2. It, too, is not the best-known approximation. Recent results by Arora & Mitchell show that there exists a polynomial-time algorithm with ratio bound of (1+ e ) for any e > 0.

1. Find the minimum spanning tree MST of the graph, the length is |Tm|
2. Locate all vertices of odd degree in MST, let O be the odd degree vertices in T
3. Find a perfect matching Tp of smallest possible length on O
4. Find a Eulerian tour T’ (visit all edges once) in Tm È Tp
5. Add shortcuts so that no city is visited more than once and output the resulting tour T.

Below is a example:

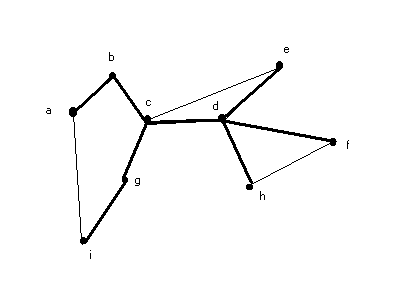
Step 1: We have a MST for 9 cities

Step 2: Odd degree vertices: a, c, e, f, h, i.

Step 3: Add the minimum weight matching ce, fh and ai and all the vertices have even degree.

Step 4: Find a Eulerian tour. T’ = a - b - c - e - d - f - h - d - c - g - i - a

Step 5: Add the shortcut, we got tour T = a - b - c - e - d - f - h - g - i - a

Christofides’ algorithm is an approximation algorithm with a ratio bound of 3/2 for the traveling salesperson problem with triangle inequality.

This algorithm use the concept of an Eulerian graph. An Eulerian graph is a connected graph in which every vertex has even degree. Eulerian graphs are precisely those graphs that contain an Eulerian tour, i.e., a cycle that passes through every edge exactly once. In order to use Eulerian graph, the minimum spanning tree T should have all even degree vertices. If the vertices in T already have even degree then no more edges are needed to turn the tree into an Eulerian graph. The only vertices we need worry about are the ones with odd degree. That is what the step 2 does. Note that there must be an even number of these odd degree vertices, since the sum of all vertex degrees must be even. Thus one way to construct an Eulerian graph that includes T would be by simply adding a matching for the odd-degree vertices (Step 3). This would increase the degree of each odd-degree vertex by one, while leaving the even degree vertices alone.

Given a set containing an even number of cities, a matching is a collection of edges M such that each city is the endpoint of exactly one edge in M. A minimum weight matching is one for which the total length of the edges is minimum.

If we add to T a minimum weight matching for its odd degree vertices, we will obtain an Eulerian graph that has minimum length among those that contain T. Therefore, in step 3, we need to find a minimum weight matching.

In step 4, we need to calculate the Eulerian tour. The length of this tour, |T’| = |Tm| + |Tp|

In step 5, we add the shortcut, so the |T| £ |T’| by using triangle inequality and we get |T| £ |Tm| + |Tp|.

We know that |Tm| £ |T_opt| (we proved this for the Approx-TSP-Tour algorithm).

Now we need to prove that |Tp| £ ½ |T_opt|.

Consider the figure shown below.

This figure shows a traveling salesman tour, with the cities that correspond to odd-degree vertices in T emphasized. The tour determines two matchings T1 and T2, indicated respectively by the bold and thin lines in the figure. The cycle is the optimal tour. By the triangle inequality, we must have:

|T_opt| ³ |T1| + |T2|

Since at step 3, the length of a minimum weight matching for the odd degree vertices of T is |Tp|, then |T1| + |T2| ³ 2 |Tp| and |T_opt| ³ 2 |Tp|. Therefore, |Tp| £ ½ |T_opt|.

Combining inequalities |T| £ |Tm| + |Tp|, |Tm| £ |T_opt| and |Tp| £ ½ |T_opt|,

we get |T| £ 3/2 |T_opt|.

Designing approximation algorithms is a very useful approach to handle NP-completeness.