Graph Algorithms – Depth First Search and it’s application in Decomposition of Graphs.
COMP 7/8713, Advanced Algorithms
Dr. Giri Narasimhan
Notes for classes on 9/21/98 and 9/23/98 --
As the name implies, the idea in Depth First Search (DFS) is to search as deep in the graph as possible, before looking at other vertices in the graph. During the depth first traversal, each vertex can be in any one of the following states –
The search begins by visiting an arbitrary undiscovered vertex, which changes the state of that vertex from "undiscovered" to "discovered", and continues till that vertex is "completely-explored". This process continues till there are no more undiscovered vertices left in the graph.
Based on these states, an algorithm for DFS can be written as follows –
DFS(G)
DFS_VISIT(G,u)
A very natural way of implementing this algorithm is to use different colors to represent different states of the vertices.
We will use the colors white to represent the "undiscovered" state, gray for "discovered" and black for "completely-explored" states.
We also maintain a counter to be able to assign time-stamps to the vertices based on the order in which they are visited. Every vertex is assigned a ‘d’ value that represents the instant at which that vertex was visited and a ‘f’ value that represents the instant at which the state of the vertex changes from "discovered" to "completely-explored", i.e the instant at which the color of the vertex changes from gray to black. This is the finish time for the vertex. We will refer to the ‘d’ value as the Depth-First search number (or DFS #) of that vertex.
Implementing these ideas, the algorithm for DFS can be re-written as follows.
DFS(G)
DFS_VISIT(G,u)
Analysis
Time complexity :- In DFS(G), the loops on lines 1-3 and 5-7 take q (n) time, where n is the number of vertices in graph G. That is, n = | V |.
Since DFS_VISIT(G,u) is invoked for every white vertex, and since the first thing DFS_VISIT(G,u) does is to change the color of u to gray, DFS_VISIT gets invoked |Adj[V] | times, or m times.
å | Adj[V] | = q (m), where m = |E|.
v Î V
The running time for DFS is therefore q (m+n).
Observations
Properties of DFS
Property 1 –
Let G=(V,E) be a connected graph. Then, DFS will visit all its vertices by calling DFS-VISIT( ) and all its edges by calling Visit_Edge( ).
This is true because, the algorithm starts by initializing all vertices to white, and DFS_VISIT(G,u) is called for every vertex in V. DFS_VISIT(G,u), visits u, and changes its color from white to gray. Thus every vertex in the graph gets visited.
In DFS_VISIT(G,u), every edge (u,v) incident on u, gets visited in the loop on line 3. Since DFS_VISIT( ) gets invoked for every vertex u in V, all edges in E get visited.
This can also be proved by contradiction. If we assume that some vertex doesn’t get visited, then at the end of the search, it’s color should be white. But, the algorithm doesn’t stop till all vertices have turned black and there is no more white vertices left, which contradicts the initial assumption.
Property 2 –
Let G = (V,E) be a connected undirected graph, and let T = (V,F) be a DFS tree of G constructed by DFS(G). Then, for every edge e Î E, either
During the search, let’s assume that we have reached a vertex u, upon which the color of u changes from white to gray. All vertices adjacent to u, can be either white or not white. In either case, the edge gets visited. If the color of the vertex v adjacent to u is white, then v gets visited and a parent pointer is set from v to u. This means that edge (u,v) is a tree edge.
If the color of v is not white and v is not the parent of u, then it means v has already been visited before u. Also it implies that edge (v,u) has not been visited, else u would have been visited earlier. Thus v cannot be colored black. Thus, v is an ancestor of u. The edge (u,v) does not get included in F, and since it connects a vertex to it’s ancestor in the graph, it’s called a back edge.
Property 3 –
Let G = (V,E) be a connected undirected graph, and let T = (V,F) be a DFS tree constructed by DFS(G), then
Intuitively, a vertex u gets discovered at time d[u] and it’s color changes from white to gray. Before u can reach the "completely-explored" state, or before it can turn black, all its descendants must have attained the "completely-explored" state. This implies that the finish time-stamp for u will be greater than the f values for all the descendants of u.
The next two properties pertain to DFS in directed graphs.
Property 4 –
Let G = (V,E) be a connected directed graph, and let T = (V,F) be a DFS tree constructed by DFS(G). Then, for every edge e Î E, either
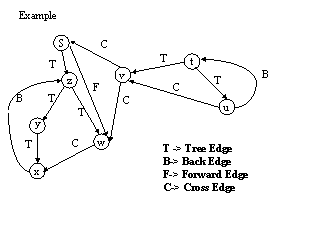
The first two cases have already been considered. An edge (u,v) is a forward edge if d[u] < d[v] and u & v are not adjacent to each other. An edge (u,v) is a cross edge if d[u] > d[v] and u is not the ancestor of v or vice-versa. Note that forward edges and cross edges never occur in the depth first search of an undirected graph.
Property 5 –
Let G = (V,E) be a connected directed graph, and let T = (V,F) be a DFS tree constructed by DFS(G). Then, for every edge e = (u,v) in the tree T, if d[u] < d[v], then v is a descendant of u.
This property is quite evident from the way DFS works. Since a vertex that is higher up in the tree gets "discovered" first, it gets a ‘d’ value that is smaller than the ‘d’ values of its descendants. Hence if d[u] < d[v] for any two vertices u and v in T, then u is an ancestor of v.
Decomposition of Graphs
The idea of graph decomposition is to partition the graph into subgraphs such that each of the subgraphs satisfies a certain desirable property.
Biconnected component : - An undirected graph is said to be connected if there is a path from every vertex to every other vertex. In other words, you would have to remove at least one vertex to disconnect the graph. This concept can be naturally extended to define biconnected graphs. An undirected graph is biconnected if there are atleast two vertex disjoint paths from every vertex to every other vertex. In other words, the connectivity of a biconnected graph is 2. Informally, a graph is biconnected if atleast two vertices need to be removed to disconnect the graph.
In general, an undirected graph is called k-connected if there are atleast k vertex disjoint paths from every vertex to every other vertex in the graph.
What is interesting is that, if a graph is not biconnected, then it can be partitioned into edge subgraphs that are biconnected.
Let G(V,E) be a connected, undirected graph that is not biconnected. A biconnected component of G is defined as a maximal biconnected subgraph of G. Here the term maximality means that no edge can be added to the subgraph and retain biconnectivity.
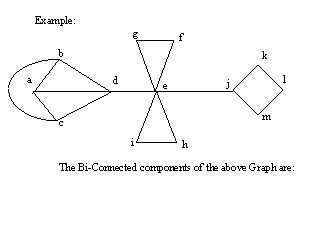
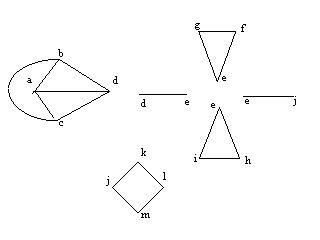
An algorithm to find all biconnected components of a graph G.
A few points need to be noted…
Menger’s theorem and Whitney’s theorem are very crucial for designing an algorithm to find all the biconnected components of an undirected graph. The implication of these two theorems is that, a graph is not biconnected if and only if there is a single vertex, the removal of which, disconnects the graph. Such a vertex is called an articulation point.
The main task of the algorithm to find all the biconnected components of a graph would be to find these articulation points in the graph. The blocks between these articulation points are the biconnected components of the graph.
Further, a biconnected component is defined as a set of edges. A vertex can belong to several components, but an edge belongs to exactly one component. In fact, each articulation point belongs to more than one biconnected component. For example, see vertex ‘e’ in the example above, which is part of four different biconnected components.
The next question to be answered is – How do we identify articulation points in a graph ?
As we already know, the algorithm DFS(G), assigns a ‘d’ value and a ‘f’ value to every vertex in the graph. In addition to these, we can compute another value called ‘low’ for every vertex u such that
Low[u] = minimum of all ‘d’ values of all vertices that are descendants of u, including u.
Now, suppose that we have calculated all the Low values, we can claim that a vertex u is an articulation point, if and only if the ‘low’ value of u is not lesser than the ‘d’ value of u. Intuitively, this means that there are no edges from vertices in the subtree rooted at u to vertices higher than u in the tree. Thus removing u would disconnect the graph and hence u is an articulation point.
Upon reaching a vertex v, the algorithm should recursively perform a DFS for all children of v, find the low values as per the definition, and at the same time decide whether a vertex is an articulation point or not.
Using all these ideas, the algorithm can be written as follows –
BICONNECTED_COMPONENTS(G,u)
The stack is mainly used to keep track of the biconnected components of the graph.

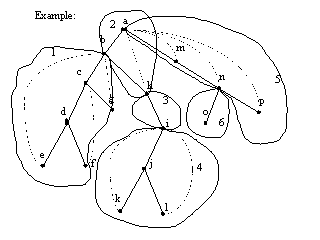
After running the algorithm on the above graph, the following are the ‘d’ and ‘f’ values for each of the vertices in the graph.
|
Vertex |
‘d’ value |
‘f’ value |
|
A |
1 |
32 |
|
B |
2 |
23 |
|
C |
3 |
12 |
|
D |
4 |
9 |
|
E |
5 |
6 |
|
F |
7 |
8 |
|
G |
10 |
11 |
|
H |
13 |
25 |
|
I |
14 |
21 |
|
J |
15 |
20 |
|
K |
16 |
17 |
|
L |
18 |
19 |
|
M |
24 |
31 |
|
N |
25 |
30 |
|
O |
26 |
27 |
|
P |
28 |
29 |
As the algorithm proceeds, the vertices and the edges traversed get pushed onto a stack. When the algorithm recognizes a biconnected component on the stack, it pops that component from the stack and gives it as output.
If we trace this algorithm, we find that the biconnected components recognized are,
This is just a partial list of the biconnected components. Proceeding in a similar way, we can obtain all the biconnected components of the graph.