Single-Source-Shortest-Path - Dijkstra's Algorithm

For shortest-path problems, we are given a weighted, directed graph G = (V, E), with weight function w: E ® R mapping edges to  real numbers.

The weight of a path p=<v₀, v₁, v₂, ...., v_k> is the sum of the weights of its constituent edges:
w(p)=S _i=1..k w(v_i-1 , v_i ),

The weight of the shortest path from u to v is

d(u,v) = w(p):u~v, if there is a path from u to v, and infinite otherwise

A shortest path from vertex u to vertex v is any path p with weight w(p) = d(u, v)

Dijkstra's Algorithm solves the single-source shortest-path problem on a weighted, directed graph for the case in which all edge weights are nonnegative, therefore we assume that w(u,v)³ 0 for each edge (u, v) Î E.
 
 

Dijkstra (G, w, s)
1. Initialize-Single-Source (G, s)
2. S ¬ Æ
3. Q ¬ V[G]
4. while Q ¹ Æ do
5.   u ¬ Extract-Min(Q)
6.   S ¬ S È {u}
7.   for each vertex v Î Adj[u] do
8.     Relax(u,v,w)
 

Initialize-Single-Source (G, s)
1. for each vertex v Î V[G] do
2. d[v] ¬ ¥
3. p [v] ¬ NIL
4. d[s] ¬ 0
 

Relax(u, v, w)
1. if d[v] > d[u] + w(u,v) then
2. d[v] ¬ d[u] + w(u,v)
3. p [v] ¬ u
 

The while loop (line 4 of Dijkstra algorithm) is executed n times.
Heap stores n values (so time complexity of all the heap operations is O(logn)) => it takes a total of O(nlogn) time

Each edge is Relaxed at most 1. This step 8 of algorithm is executed O(m) times.

It is important to note that Relax is not a constant time operation. Priority queue Q has to be updated every time a key value is updated. Thus each call to Relax will need heap operations which take O(logn) time. Hence its time complexity is O(mlogn).

This algorithm looks pretty much the same as Prim's algorithm. The difference is that here we have a different distance function.

All-Pairs-Shortest-Path

• input: Graph G , weight matrix W
• output: length of shortest path between all pairs of vertices
• the output will be represented using a square matrix D of size n x n: D_nxn , where

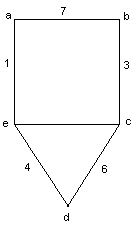
For example, if the following graph is given

the weight matrix for the graph is:
 

0	7	¥	¥	1
7	0	3	¥	¥
¥	3	0	6	2
¥	¥	6	0	4
1	¥	2	4	0

 

The following subroutine will be used by the All-Pairs-Shortest-Paths algorithms shown below.
 

Extend-Spath (D,W)
1. n ¬ rows[D]
2. let D’ be an n x n matrix initialized to µ
3. for i ¬ 1 to n do
4.    for j ¬ 1 to n do
5.       for k ¬ 1 to n do
6.          d’_ij ¬ min(d’_ij, d_ik + w_kj)
7. return D’
 
 

Let d _ij ^(k) = length of a shortest path from i to j such that it uses at most k edges.

The recurence to go from the k-1^th iteration to the k^th iteration is:
d_ij^(k) = min_l{ d_il^(k-1)+w(l,j) }

W = D⁽¹⁾ ® D⁽²⁾ ® D⁽³⁾ …. ® D⁽ⁿ⁾

The algorithm for this is:

All-Pairs-Shortest-Paths-1 (G,W)
1. n ¬ rows[W]
2. D⁽¹⁾ ¬ W
3. for m ¬ 2 to n-1 do
4.    D^(m) ¬ Extend-Spath (D^(m-1), W)
5. return D^(n-1)
 
In this case we have n iteration, so the time complexity is O(n⁴)
 

Another way to do this is by D⁽¹⁾ ® D⁽²⁾ ® D⁽⁴⁾ ® D^{(8) ® …}

Here the necessary recurence is:

d_ij^2(k-1) = min_l{ d_il^(k-1)+d^(k-1)(l,j) }

 
The resulting algorithm is as follows:

All-Pairs-Shortest-Paths-2 (G,W)
1. n ¬ rows[W]
2. D⁽¹⁾ ¬ W
3. for m ¬ 1 to logn do
4.    D^(2m) ¬ Extend-Spath (D^(2m), D^2(m-1))
5. return D^(n-1)
 
In this case we have logn iteration, so the time complexity is O(n³logn)
 

There is an interesting thing to notice with this algorithm. There exist a similarity between matrix multiplication and All-pairs-shortest-Path algorithm. Here are both, side-by-side:
 

Extend-Spath (D,W)  1. n ¬ rows[D] 2. let D’ be an n x n matrix initialized to ¥  3. for i ¬ 1 to n do 4.    for j ¬ 1 to n do 5.       for k ¬ 1 to n do 6.          d’ij ¬ min(d’ij, dik + wkj) 7. return D’

Matrix-Multiply (A, B)  1. n ¬ rows[A] 2. let C be an n x n matrix initialized to 0 3. for i ¬ 1 to n do 4.    for j ¬ 1 to n do 5.       for k ¬ 1 to n do 6.          cij ¬ cij + aik * bkj) 7. return C