Comp 7/8713 Lecture Notes
Computational Geometry
By
Sunny Tara
Overview:-
Introduction to Computational Geometry
Computational Geometry is a branch of computer Science that studies algorithms for solving computational problems on geometric objects. Such as points, lines, triangles etc.
Properties: extent, intersection, proximity relationships
Applications: graphics (e.g., hidden line removal)
A field full of easily stated problems which humans seems to be able to solve extremely easily, but for which the "obvious" algorithms are often quite slow.
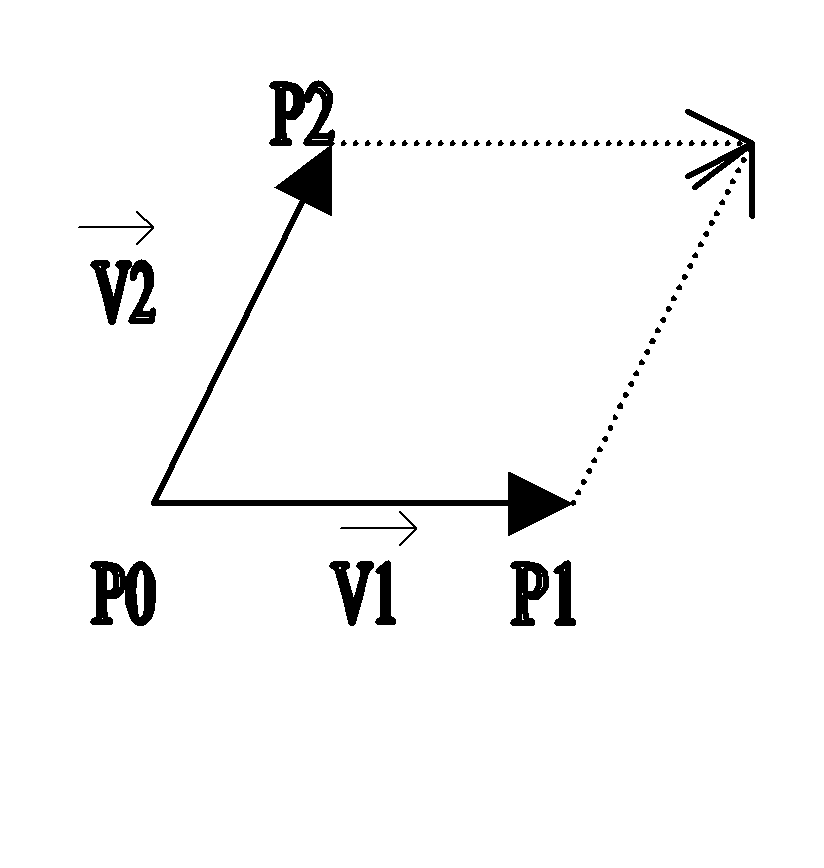
Cross Product
Let P0 = (0,0) P1 = (x1,y1) P2= (x2,y2). Let V1 = PoP1 and V2 = P1P2
Then the cross product V1 X V2 will be x1y2 – x2y1. Which is also the determinant of the matrix
| x1, y1|
| x2, y2|

Magnitude V1 X V2 = det | V1. V2|
To determine whether the given cross product is clockwise or counterclockwise can be determined using the right hand rule along the z axis. If it is negative then it is counterclockwise. If is positive then it is clockwise.
If V1 X V2 is > 0 then it is counterclockwise
If V1 X V2 is < 0 then it is clockwise
We use the cross product to solve two simple problems below.
Problem
In going from P0 to p1 to p2 do you make a right or left turn?
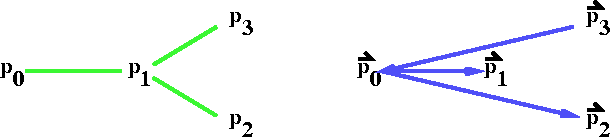
Solution
This problem can be easily solved using the right hand rule, since PoP1 X P1P2 < 0. It is clockwise and involves a right turn. If we look at
PoP1 X P1P3 > 0 which is counterclockwise, in this case we would make a left turn.
Problem
Given two line segments P1P2 & P3P4 do they intersect?
Solution
The naïve algorithm works as follows: compute equations of the lines that point of intersection that contain the 2 segment. We then solve for the two equations, find the point of intersection and then check if that point lies on the line segment P1P2. An improved algorithm is proposed below. It involves two steps.
The second test can be solved using the Cross product, which is better solution because of precision. The naïve algorithm involves divisions, which is, in general, not very precise. Cross product computations eliminate the need to perform divisions. It only involves some multiplication's, additions and a test whether a number is positive or negative.
Example.
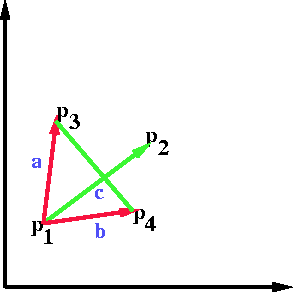
In the above example a X c < 0 and b X c > 0. They have different signs. This implies that the segment P3P4 straddles the line containing P1P2. It does not necessarily imply that the 2 segment intersects
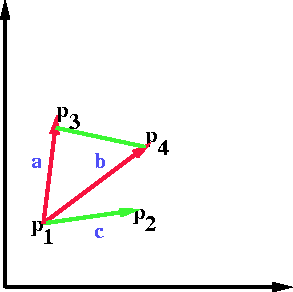
In the above example a X c < 0 and b X c < 0. They have same signs. Thus the segment P3P4 the line containing P1P2. Consequently P1P2 & P3P4 cannot intersect.
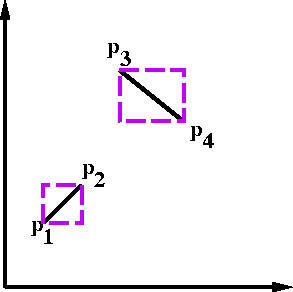
In the above example, a simpler test for intersection fails, i.e. the bounding boxes do not intersect.
Convex Hull
The convex hull of a given set of points is the smallest convex polygon containing all of them.
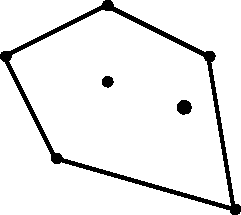
Graham’s Scan Method.
This method exploits the idea that walking around the hull in counterclockwise direction involves all left turns and no right turns.
Basic idea.
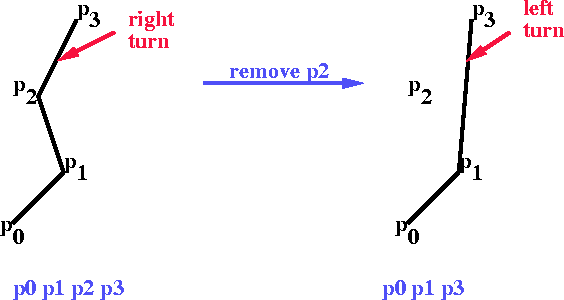
In this example above going from P1 to P2 to P3 involved right turn, implying that P2 would not be a point on the convex hull. The right hand side shows the situation after P2 is removed.
GRAHAM-SCAN( Q)
Note that SECOND(S) returns the item on S that is second from top. It does not remove the item. Top(S) returns the top item of the stack without removing it.
Example of Graham-scan is given on page 900-901 of the CLR book.
Proof of Correctness:
Given on page 903 of CLR book
Time Complexity is O (n lg n)
Jarvis’s March or package-wrapping algorithm.
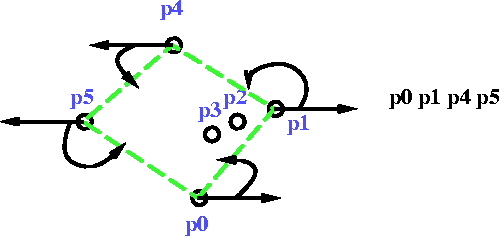
Basic Idea
The first vertex chosen is the lowest point p0. The next vertex p0 has the least polar angle subtended by a point at Po with respect to the positive x-axis. The right chain goes as high as the point p4, Then the left chain is constructed by finding the least polar angles with respect to the negative x-axis.
JARVIS’S MARCH
Analysis:-
Both the while loop takes total of h times, where h is the number of points on the convex hull. Body of while loop takes O (n) to compute minimums.
This algorithm takes O (nh)
CLOSEST PAIR PROBLEM
Divide and conquer Approach
Divide: find a vertical line that bisects the set [O (n)]
Conquer: recursively solve 2 subproblems; find min 2T(n/2)
Combine: take care of pairs on either side of bisector. Closet pair is either the pair with distance d found by one of the recursive calls, or it is a pair of points that lie on either side of the bisector and close to the bisector. Look at fig 35.12(a) on page 910 of CLR.
Basic Idea
Given P points. Let array X and Y contains all the points of the input subset P. The points in X array are sorted so that their x – coordinates are monotonically increasing. Similarly, Y array is sorted by monotonically increasing y – coordinate. The vertical line that divides the point set P in two half sets Pl and Pr. So,all the points on pl are on or to the left of vertical line and all points in Pr are on or to the right of vertical line. The array X is divided into array Xl and Xr, Which contains the points of Pl and Pr respectively, sorted by monotonically increasing x-coordinate. Similarly, the array Y is divided into arrays Yl and Yr which contains the points of Pl and Pr respectively, sorted by monotonically increasing y-coordinate
Having divided P into Pl and Pr, it makes two recursive calls, one to find the closest pair of points in Pl and the other in Pr. The inputs to the first call are the subset Pl and arrays Xl and Yl, the second call receives the inputs Pr, Xr and Yr . Let the closest-pair distances returned for Pl and Pr be ![]() and
and ![]() and let
and let ![]()
![]()
![]()
![]() The closest pair is either the pair with distance
The closest pair is either the pair with distance ![]() found by one of the recursive calls, or it is a pair of points with one point in Pl and the other point in Pr. The algorithm determines if there is such a pair whose distance is less that
found by one of the recursive calls, or it is a pair of points with one point in Pl and the other point in Pr. The algorithm determines if there is such a pair whose distance is less that ![]() . If there is a pair of points with distance less than , both points of the pair must be within
. If there is a pair of points with distance less than , both points of the pair must be within ![]() units of vertical line. Thus the points must reside in 2
units of vertical line. Thus the points must reside in 2![]() wide vertical strip centered at the vertical line that divides P into Pl and Pr.
wide vertical strip centered at the vertical line that divides P into Pl and Pr.
To find such a pair the algorithm does the following
The key to presorting x and y coordinates before the first recursive call is that it adds an additional O (n lg n) to the running time but now each of the recursion it only takes linear time.
ALGORITHM
Note that if all pairs of points on either side of the bisector are considered, then the combine step would take O(n^2) time.
More detail algorithm is given on page 910 of the CLR book
Closest-Pair(P, x, y)
Given on page 910 of the CLR book
Proof of Correctness
Given on page 910 of the CLR book
Analysis
Initial Sorts: O (n lg n), Closest Pair: 2T(n/2) + O(n)
This algorithm takes O( n lg n) times.
Line Segment Intersection
Problem:
Given n horizontal and m vertical line segment, find all intersections among them.Solution
Naïve Algorithm would take O(mn) time.
Basic idea
We will sweep a vertical line from left to right. We will inductively assume that all intersections to the left of the sweep line have been processed and reported. In order to process future intersections to the right of the line, we maintain a data structure (RB tree) that maintains the y coordinates of all horizontal lines that intersect the sweep line. Note that the situation changes as the line is swept, but these changes happen only at discrete x co-ordinate. In order to predict all these changes, a queue Q of events is also maintained. It is sufficient to notice that all such changes happen at the start or end x co-ordinates of horizontal lines and at the x-co-ordinates of vertical lines.
LINE SEGEMEN INTERSECTION (V,h)
Note: Range query :- The range-query(D,low(vi),high(vi)) will gives all the points in query range [low(vi) : high(vi)]. let ![]() and
and ![]() ’ be the two leaves where the searches end. Then the point in interval [low(vi) : high(vi) ] are the ones stores in the leaves between
’ be the two leaves where the searches end. Then the point in interval [low(vi) : high(vi) ] are the ones stores in the leaves between ![]() and
and ![]() ’. The figure below gives an example for the range query [17 :80].
’. The figure below gives an example for the range query [17 :80].
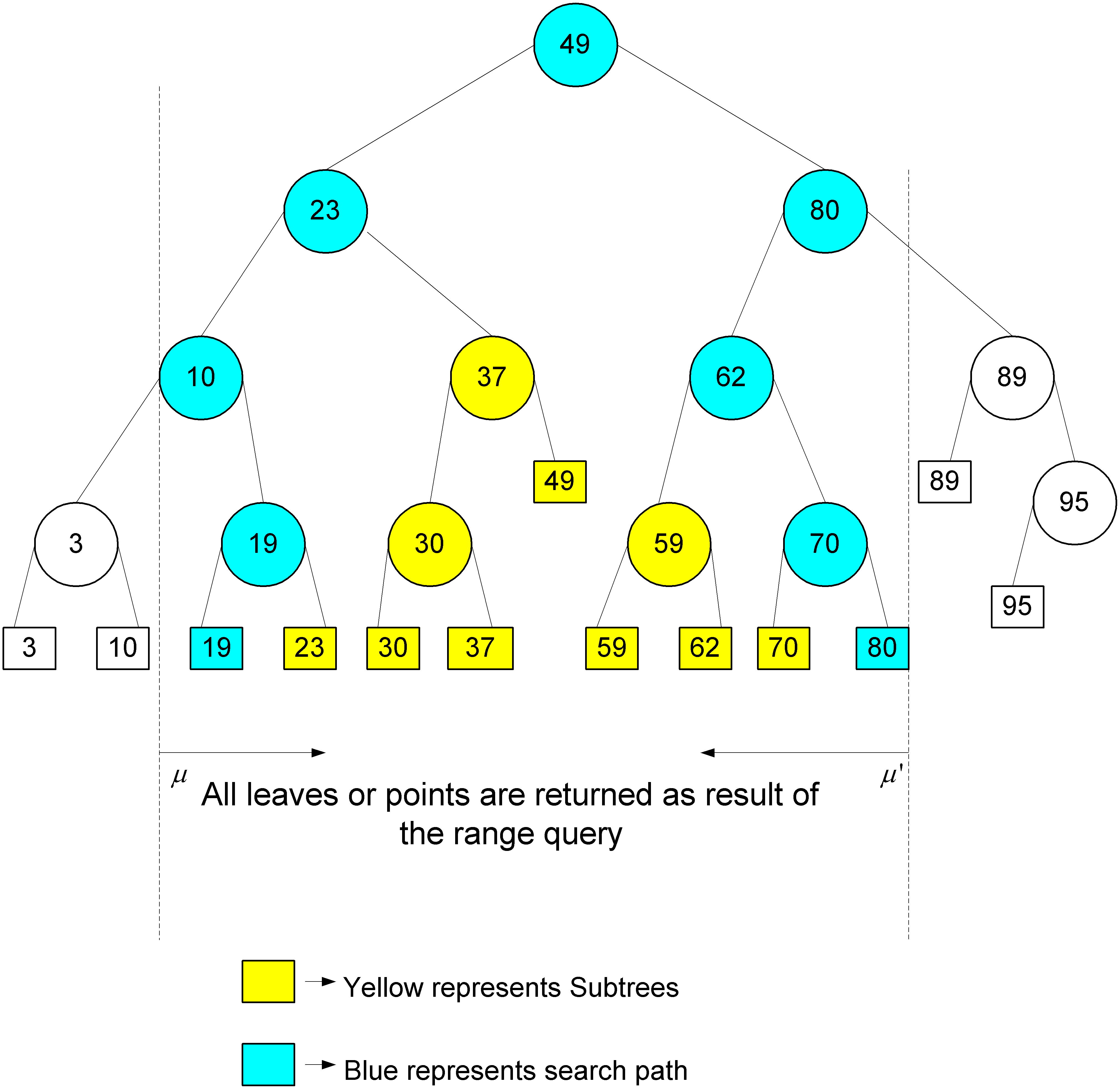
Proof of Correctness
Theorem 35.1 given on page 896 in the CLR
Analysis
Sort segments O (n lg n)
n RB-Inserts O (n lg n)
n RB-Deletes O (n lg n)
O(1) comparison
The algorithm takes O (n lg n).