Note_Oct14

Algorithm Note, Oct 14 Wenjian Yang

Recap:

Problem: To prove clique is a NP-complete problem

Solution:

We show the following:

Proof that clique is in NP. A possible certificate is a set of vertices; the verification algorithm will only need to check if the set forms a clique or not, which can be done in time polynomial in the number of vertices.
A reduction from 3SAT to clique, i.e. given an instance of 3SAT, we need to show a reduction that constructs an instance of clique. We need to prove that the 3SAT instance is satisfiable if and only if there’s a solution to the clique instance.
Proof that a reduction runs in polynomial time.

(Detailed proof can be found on page 947 – 949 in the textbook)

Note: The key to the above proof is an appropriate reduction. The reduction needs to ensure the "if and only if" relationship.

Vertex Cover (VC)

Definition: Given a graph G(V, E), a vertex cover S is a subset of V, that covers all the edges in E. The size of a vertex cover is the number of vertices in it.

Instance: Graph G(V, E), and an integer k

Question: Does the graph G have a vertex cover of size k?

Observation: By definition, for any edge, one of its two ends should be included in the vertex cover. If we remove the vertex cover and all the edges covered by it from the graph, there will be no edges left between any pair of the remaining vertices; otherwise, such an edge is not covered by any vertex in the vertex cover.

Now we prove that vertex cover problem is NP-complete, following the three steps.

Proof:

Vertex-cover is in NP

A possible certificate is a subset of vertices V’ from the graph G(V, E). The verification algorithm first checks the size of V’ is k; then it checks for each edge (u,v) in E, whether u or v belongs to V’. This verification can be performed in polynomial time. So vertex-cover is in NP.

Reduce from clique to vertex-cover.

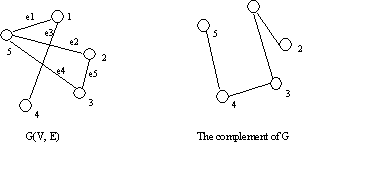
We define the complement of G as (V, ), where = {(u, v) : (u, v) ). Give an instance <G(V, E), k> of the clique problem, the reduction algorithm compute the complement . The output of the reduction algorithm is the instance <, |V| - k> of the vertex-cover problem. To prove the above claim, we need to show that the graph G has a clique of size k if and only if the graph has a vertex cover of size |V| - k.

Prove:

Suppose that G has a clique V’ V with |V’| = k. We claim that V – V’ is a vertex cover in . Let (u, v) be an edge in , i.e. (u, v) . This implies that at least one of u or v does not belong to V’, since every pair of vertices in V’ is connected by an edge of E. This also means that at least one of u or v is in V – V’, which means that edge (u, v) is covered by V – V’. This is true for all the edges of , i.e. every edge of is covered by a vertex in V – V’. Hence, the set V – V’ forms a vertex cover for , it has size |V| - k.
On the other hand, suppose graph has a vertex cover V’, where |V’| = |V| - k. Then, for all u, v V, if (u, v) , at least one of u or v V’. This implies that for all u, v V, if u V’ and v V’, then (u, v)

E. In other words, V – V’ is a clique, and it has size |V| - |V’| = k.

The reduction will take polynomial time, since we only need to compute the complement of the given graph.

Note:

Decision problem vs. optimization problem.

We could always transform an optimization problem into a series of decision problems. For example if we are asked to find the minimum size among all vertex covers for a given graph, we can try to solve a series of decision problems such as whether the graph has a vertex cover of size k (k = 1, 2… n). If we could solve the decision problem in polynomial time, we need only to repeat the procedure at most n times to solve the optimization problem. (If we use some tricks such as binary search, we only need to solve at most log(n) decision problems) .

Suppose we could solve the vertex cover problem in polynomial time and we know the minimum size in all the vertex covers for a given graph is k, we would like to find such a vertex cover of size k. We can remove a vertex u and all the edges covered by u from the graph, then compute the minimum size in all the vertex covers for the remaining portion of the graph. If the minimum size is k, then the vertex we just removed does not belong to the optimal vertex cover; otherwise it belongs to the optimal vertex cover. Repeat the above procedure for all the vertices in the graph, we can find an optimal vertex cover of the minimum size k. If we could solve the vertex cover problem in polynomial time, we could also find a such an optimal solution in polynomial time.

Subset Sum (SS)

Instance : Given S = {X₁, X₂, …, X_n}, a set of integer numbers and an integer number t.

Question: If there’s a subset S’ S, such that S X_i = t.

Prove this problem is NP-Complete.

Proof:

subset-sum is in NP.

A possible certificate is a subset S’ S. A verification algorithm simply check if the sum of all elements in S’ equal to t, which will take polynomial time. So SS is in NP.

Reduce from vertex-cover to subset-sum.

Given an instance <G, k> of the vertex-cover problem, the reduction algorithm constructs an instance <S, t> of the subset-sum problem such that G has a vertex cover of size k if and only if there is a subset of S whose sum is exactly t.

The key to the reduction is an incidence-matrix representation of G. Let G(V, E) be an undirected graph and let V = {v₁, v₂, … v_n} and E = {e₁, e₂, …, e_m}. The incidence matrix of G is a n*m matrix B(b_ij), such that

b_ij = 0 if edge e_j is incident on vertex v_I

1 otherwise

Given a graph G and an integer k, the reduction algorithm computes a set of numbers S and an integer t. All the numbers have m+1 digits, and a "modified-base-4" is used to represent these numbers. The m low-order digits of a number will be base-4, while the high-order digit can be as large as k. The set of numbers is constructed in such a way that no carries can be propagated from lower digits to higher digits.

The set S consists of two types of numbers, {x} and {y} , corresponding to vertices and edges respectively. For each vertex v_iV, we create a positive integer xi whose high-order digit is 1 and the low-order digits correspond to v_i’s row of the incidence matrix B. For each edge e_j E, we create a positive integer y_j whose high-order digit is 0 and the low-order digits correspond to the e_j’s row of the identity incidence matrix (the identity incidence matrix is the m * m matrix with 1’s only in the diagonal positions.)

The first digit of the target sum t is k, and all m low-order digits are 2’s.

If we transform both the set S and the target t into the base-10 representation, we have the following:

Xi = 4^|E| + i = 1, 2, …, n

Yj= 4^j j = 1, 2, …, m

T = k * 4^|E| +

We need to show that graph G has a vertex cover of size k if and only if there is a subset S’ S whose sum is t.

Before get into the proof, we observe that for each edge e_j E, there are three 1’s in set S in the e_j column: one from each of the two vertices incident on e_j, and one from y_j.

Suppose that G has a vertex cover S’ S of size k. Let V’ = {v_i1, v_i2, …, v_ik}, and define S’ = {x_i1, x_i2, …, x_ik} U {y_j : e_j is incident on precisely one vertex in V’}.

The sum of the k leading 1’s from x_im S’ gives the leading digit k of the modified base-4 representation of t. For all the low-order digit the sum from S’ will give all 2’s. Because V’ is a vertex cover, each edge e_jE is incident on at least one vertex and at most two vertices in V’, so we have to select at least one vertex in V’. If e_j is covered by exactly one vertex in V’, we will select y_jaccording to the rule, we get a sum equal to 2; if e_j is covered by two vertices in V’, according to the rule, we still get the sum equal to 2. So the summation on the low-order digits can only be all 2’s. Thus S’ is a solution to the subset-sum instance S.

Suppose that there’s a subset S’

S that sums to t. Let S = {x_i1, x_i2, …, x_im} U {y_j1, y_j2, …, y_jp}. We claim that m = k and that V’ = {v_i1, v_i2, …, v_im) is a vertex cover for G. Since we use modified-base-4 representation, there are no carries from one position to the next position. For each of the m low-order positions of t, at least one and at most two x_i must contribute to the sum. Since at least one x_i contributes to the sum for each edge, we see that V’ is a vertex cover. The only way the leading k in target t can be achieved is by selecting exactly k of the x_i in the sum, thus the size of the vertex cover is k.

Vertices 2, 4, 5 build a vertex cover for the given graph. X2 + X4 + X5 = 3754 gives a solution to the subset-sum problem with target value 3754	.			Modified base 4					base 10
				e1	e2	e3	e4	e5	S
		X1 = V1	1	1	0	1	0	0	1296
		X2 = V2	1	0	1	0	0	1	1089
		X3 = V3	1	0	0	0	1	1	1029
		X4 = V4	1	0	0	1	0	0	1040
		X5 = V5	1	1	1	0	1	0	1348

		Y1 = e1	0	1	0	0	0	0	256
		Y2 = e2	0	0	1	0	0	0	64
		Y3 = e3	0	0	0	1	0	0	16
		Y4 = e4	0	0	0	0	1	0	4
		Y5 = e5	0	0	0	0	0	1	1

		t	3	2	2	2	2	2	3754

The reduction runs in P

"All of these numbers have polynomial size when we represent them in binary. The reduction can be performed in polynomial time by manipulating the bits of the incidence matrix." (P953 in textbook)

Note:

In the above subset-sum problem we used integer space, the subset-sum problem in the real space is also NP-Complete, since it is a superset of the problem we are dealing with above.

Hamiltonian-cycle problem (HAM-CYCLE)

Instance: G(V, E), which is an unweighted graph.

Question: Does G have a hamiltonian circuit?

Definition: A hamiltonian cycle of an undirected graph G (V, E) is a simple cycle that contains each vertex in V. (simple cycle implies an edge can be used at most once)

Proof:

HAM-CYCLE is in NP

A possible certificate is a set of vertices with ordering. The verification algorithm first checks if we can get a hamiltonian cycle following the order given in the vertices set. It will take polynomial time.

Reduce from 3SAT to HAM-CYCLE

Basically we need to construct two widgets to build a graph from a 3SAT problem.

Widget A:

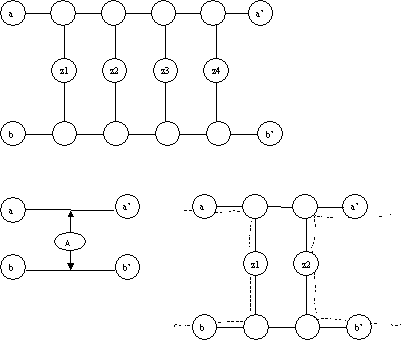
This equipment ensures that if we want to traverse all the vertices just once we can only enter (leave) from a and leave (enter) from a’ or enter (leave) from b and leave (enter) from b’. We can not enter from a and leave from b. This is useful to present X and X complement.

If we only have two layers, we could traverse all the points using two segments (see above). So we need at least four layers to control the path.

Widget B (page 956) is more complicated, and it is constructed to represent a clause.

The study of HAM-CYCLE problem will continue in the following class.

Most of the contents for this class can be found in the textbook from page 946 to page 955. Please refer to the textbook for more detailed explanations.