Device A (Figure 1) is subgraph in G.
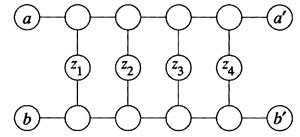
Figure 1 Device A
It includes 12 vertices, and is connected with the rest part of G only
through vertices a, a', b, b'. Also, we can represent device A as the compact
version in Figure 2.
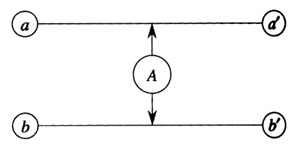
Figure 2 Compact version of device A
We use device A to make sure that only one of the edges of the pair
of edges (a,a') and (b,b') can be included in the hamiltonian cycle.We
select even number of z edges (z1-z4). Because hamiltonian cycle must cover
every vertex in device A exactly once, so we can enforce that just one
edge of the edges from (a,a') and (b,b') can be used. The two possibilities
are alternately animated in Figure 3.
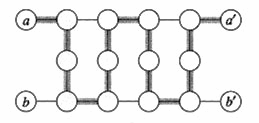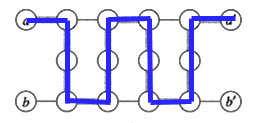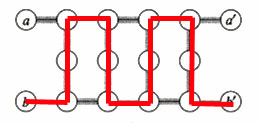
Figure 3 Just use one edge in device A
Device B (Figure 4) is another subgraph in G.
Figure 4 Device B
This device B is connected to the remainder graph of the G through vertices
b1 ~ b4. Figure 5 is a compact version of device B. Inside it, at least
one of the paths pointed by the arrows must be in the hamiltonian cycle.
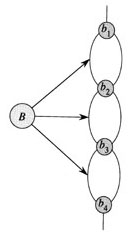
Figure 5 Compact version of device B
Because of the structure of device B (Figure 4), you can not use all of the edges (b1, b2), (b2, b3),(b3, b4) in a hamiltonian cycle (at least one of them can not be used). It should cover all the vertices in device B. So, on the other hand, at least one of the paths pointed by the arrows (Figure 5) must be used. The hamiltonian cycle of G could traverse any proper subset of the edges in device B. Figure 6 shows five such subsets.
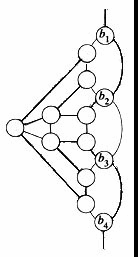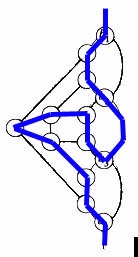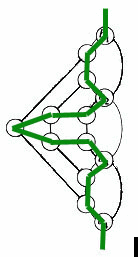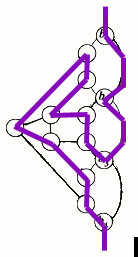
Figure 6 Five subsets in hamiltonian cycle of device B.
Main idea:
Now we show how to reduce the 3-CNF-SAT problem to the HAM-CYCLE problem. We use the two devices, A and B, to do the reduction. The main idea is that from 3-CNF formula f, we can construct a graph G, and try to find HAM-CYCLE in it. First, we use a device B to present each of the k clauses in the 3-CNF formula f. We link these B devices in the series, by connecting bi,4 to bi+1,1. Device bi expresses the ith clause. For each variable xm in formula f, we use two vertices xm' and xm", and connect them by two edges; one corresponds to assigning value 1 to xm, and the other corresponds to assigning value 0 to xm. We link them all in series. Finally, we connect the two parts: clauses part and value assignment part together by edges at the top and the bottom. Finally, we need to impose the constraint that if variable xm is assigned a value, this value is used in each of the clauses it appears in. Thus we use A devices to express the constraints on xm.
Example:
We use a example to explain it. Please look at the Figure 7.
Figure 7 Graph for formula f=(¬x1
È x2 È ¬x3)
Ç (x1 È ¬x2
È
x3)
Ç (x1
È x2 È ¬x3)
and x1 =0, x2 =1,
and x3 = 1.
Consider the 3-CNF formula is f=(¬x1 È x2 È ¬x3) Ç (x1 È ¬x2 È x3) Ç (x1 È x2 È ¬x3), and question is if there is true assignment for it. We note that the possible true assignments include:
(1) x1 =0, x2 =1, and
x3 = 1.
(2) x1 =1, x2 =1,
and x3 = 1.
(3) x1 =1, x2 =1,
and x3 = 0.
Consider the assignments in (1). For x1 =0, x2 =1, and x3 = 1, in the right part of the graph, we select the edges ~e1(0), e2(0), and e3(0). Now we reach the bottom of the graph.
How to use B device:
Now we reach the B devices part. Each B device can express one clause; because in B device, at least one of left edges (I think we can call them true edge, which is the path pointed by the arrows in Figure 5) must be used. This means if we want (b1 È b2 È b3) be true, at least one of b value should be true. For the three variables, we need 4 vertices and 3 pairs of edges in B device.
How to use A device:
We use A devices to relate variables to the clauses. If the jth literal of clause Ci is xm, we use an A device to connect left part's edge (bi,j, bi,j+1) with the right part's edge em. If the jth literal of clause Ci is ¬xm, we use an A device to connect left part's edge (bi,j, bi,j+1) with the right part's edge ~em. Here, we use the device A's property that just one edge of the pair of edges can be and must be used. This means, if jth literal is xm, if xm=1 (select em), the literal should be true (select left edge in device B); otherwise, if xm=0(select ~em), the literal should be false (select right edge in device B). In the other condition, if jth literal is ¬xm, if xm=1(select em), the literal should be false (select right edge in device B); otherwise, if xm=0(select ~em), the literal should be true (select left edge in device B).
For example, in the 3rd clause, the 3rd literal is ¬x3; so we use A device to connect ~e3 and the right edge which is between b3,3 and b3,4 in the B device. When x3 is true (select e3, not ~e3), edge between b3,3 and b3,4 must be selected.
In the right part, several A devices could be connected to one em or ~em edge. In this case, we connect A devices in series, as Figure 8.
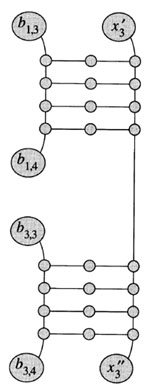
Figure 8 A piece of actual subgraph in which two A devices connected
to one edge.
Putting them all together:
Figure 7 schematically described the complicated graph constructed by the reduction. Every A device has 12 vertices, and every B device has 9 devices.The hamiltonian cycle should cover all the vertices in the graph.
We can find other hamiltonian cycles from other true assignments for formula f, such as: x1 =1, x2 =1, and x3 = 0.
Proof:
In previous process, we showed how to construct a graph G from a formula f. If a formula f is satisfiable, we can construct a hamiltonian cycle for the graph G. First, use the truth assignment to decide the road in the right part of the graph: if xm=1, select em, otherwise select ~em. Then, in the left part, we can find a road to go through the B devices; because every B device corresponds to a clause, and in every clause there must be at least one literal is true, that is what B device needs.
On the other hand, if graph G contains a hamiltonian cycle, we can claim that formula f is satisfiable. From the right part of the graph, we can find the true assignment set from the cycle's choice between em and ~em set. By using this assignment, we can definitely satisfy the formula f. This is because the cycle can pass the B devices in the left part, that means in every clause, there must be at least one literal is true. So, total formula f is satisfiable.
Thus for a unsatisfiable formula, no hamiltonian cycle exists in the graph.
So, we can reduce the 3-CNF-SAT problem to the HAM-CYCLE problem.