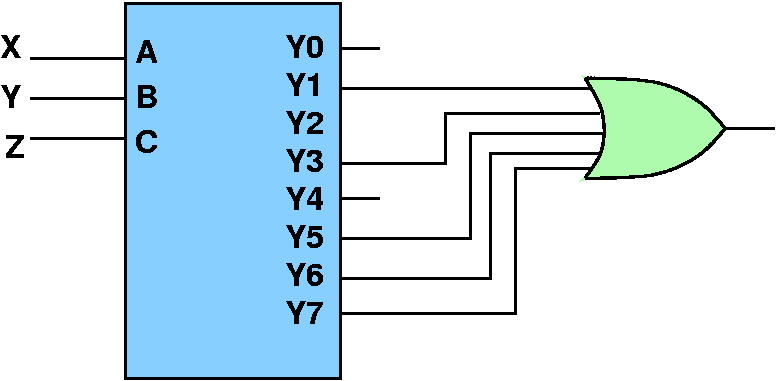
Function:
AC' + BC'
Answer:
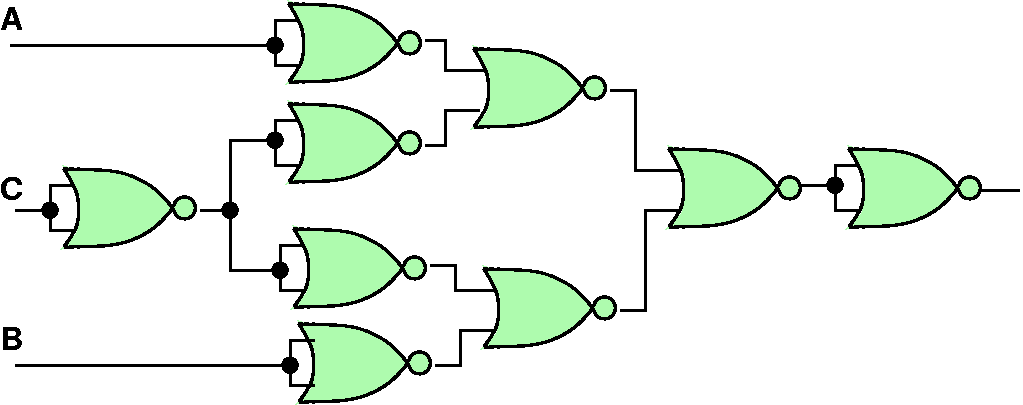
For the following given boolean functions, use a Karnaugh Map to find a minimal, but equivalent function. Also draw the resulting circuit.
Given:
F(X,Y,Z) = X'YZ' + X'YZ + XYZ' + XYZ + XY'Z
Answer:
F(X,Y,Z) = Y + XZ
Given:
F(W,X,Y,Z) = W'X'Y'Z' + W'X'Y'Z + W'X'YZ + W'XYZ + WX'Y'Z'
+ WX'Y'Z + WX'YZ' + WXYZ
Answer:
F(W,X,Y,Z) = X'Y' + W'X'Z + XYZ + WX'Z'
Given:
F(X,Y,Z) = X'Y'Z + X'YZ + XY'Z + XYZ' + XYZ
Answer:
F(X,Y,Z) = Z + XY
Given:
F(A,B,C,D) = A'B'C'D + A'BCD + AB'C'D + ABC'D + ABCD
Answer:
F(A,B,C,D) = B'C'D + BCD + ABD
OR
F(A,B,C,D) = B'C'D + BCD + AC'D
Given:
F(W,X,Y,Z) = W'X'Y'Z' + W'X'YZ' + W'XY'Z + W'XYZ
+ WX'Y'Z' + WX'YZ' + WXY'Z + WXYZ
Answer:
F(W,X,Y,Z) = XZ + X'Z'
Given:
F(A,B,C,D) = A'B'C'D + A'BC'D' + A'BC'D + A'BCD
+ ABC'D' + ABCD' + ABCD
Answer:
F(A,B,C,D) = BC'D + BCD + A'BC' + ABD'
OR
F(A,B,C,D) = BC'D + A'BD + BC'D' + ABC
OR
F(A,B,C,D) = BC'D + BCD + BC'D' + ABD'
OR
F(A,B,C,D) = BC'D + BCD + BC'D' + ABC
Given:
(AB')'
Result:
A' + B
Given:
(X'YZ' + X'Y'Z)'
Result:
(X + Y' + Z)(X + Y + Z')
Given:
(XY + Z)(Y + XZ)
Result:
XY + XYZ + YZ + XZ
Compute the duals of the following given boolean expressions.
Given:
AB + C'D + E'
Answer:
(A + B)(C' + D) E'
Given:
(A + 1)(B0 + C)
Answer:
(A0) + ((B + 1) C)
Given:
(A' + B0 + 1)(AB' + C) D + A'B
Answer:
((A' (B + 1) 0) + ((A + B') C) + D)(A' + B)
Function:
AC' + BC'
Answer:

Function:
F(X,Y,Z) = X'YZ' + X'YZ + XYZ' + XYZ + XY'Z
Answer:
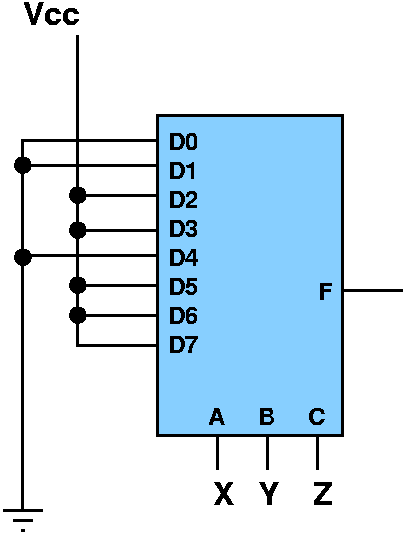
Function:
F(X,Y,Z) = X'Y'Z + X'YZ + XY'Z + XYZ' + XYZ
Answer:
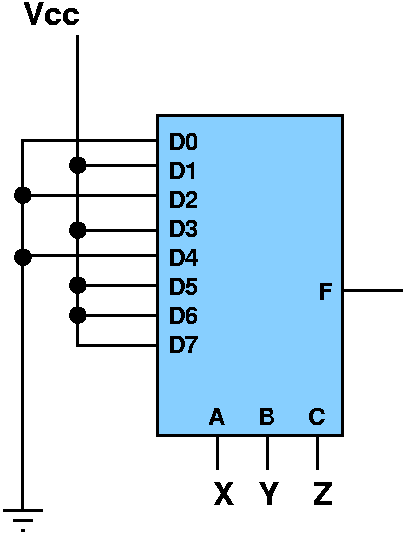
Function:
F(X,Y,Z) = X'YZ' + X'YZ + XYZ' + XYZ + XY'Z
Answer:
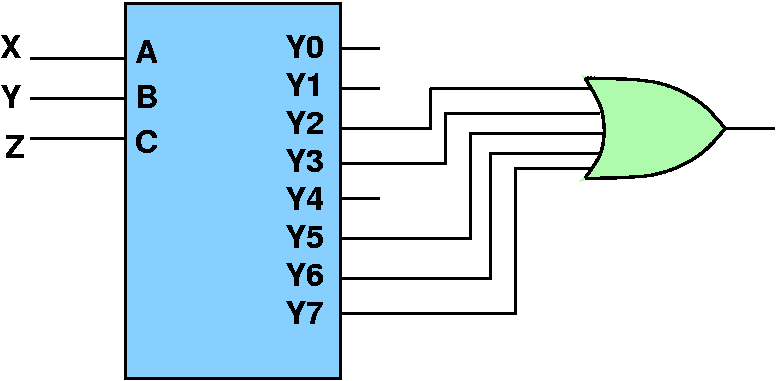
Function:
F(X,Y,Z) = X'Y'Z + X'YZ + XY'Z + XYZ' + XYZ
Answer: