CDA-4101 Lecture 14 Notes

Scientific Notation for Real Numbers

desire to separate the numeric range from the numeric precision
floating point borrows from scientific notation
```
    n = f x 10^e
  
```
"f" is the fraction (precision) and "e" the exponent (range)

Floating Point and Real Numbers

floating point is used as a model for real numbers
floating point is an approximation of the real numbers
only a finite number of possible numbers

Floating Point Example

only one digit and sign for fraction
only one digit and sign for exponent

Col. 0	Col. 1	Col. 2	Col. 3	Col. 4	Col. 5	Col. 6
0	0.0000007	0.0005	0.3	100	80000	60000000
0.000000001	0.0000008	0.0006	0.4	200	90000	70000000
0.000000002	0.0000009	0.0007	0.5	300	100000	80000000
0.000000003	0.000001	0.0008	0.6	400	200000	90000000
0.000000004	0.000002	0.0009	0.7	500	300000	100000000
0.000000005	0.000003	0.001	0.8	600	400000	200000000
0.000000006	0.000004	0.002	0.9	700	500000	300000000
0.000000007	0.000005	0.003	1	800	600000	400000000
0.000000008	0.000006	0.004	2	900	700000	500000000
0.000000009	0.000007	0.005	3	1000	800000	600000000
0.00000001	0.000008	0.006	4	2000	900000	700000000
0.00000002	0.000009	0.007	5	3000	1000000	800000000
0.00000003	0.00001	0.008	6	4000	2000000	900000000
0.00000004	0.00002	0.009	7	5000	3000000	1000000000
0.00000005	0.00003	0.01	8	6000	4000000	2000000000
0.00000006	0.00004	0.02	9	7000	5000000	3000000000
0.00000007	0.00005	0.03	10	8000	6000000	4000000000
0.00000008	0.00006	0.04	20	9000	7000000	5000000000
0.00000009	0.00007	0.05	30	10000	8000000	6000000000
0.0000001	0.00008	0.06	40	20000	9000000	7000000000
0.0000002	0.00009	0.07	50	30000	10000000	8000000000
0.0000003	0.0001	0.08	60	40000	20000000	9000000000
0.0000004	0.0002	0.09	70	50000	30000000
0.0000005	0.0003	0.1	80	60000	40000000
0.0000006	0.0004	0.2	90	70000	50000000

Floating Point Example: Exceptions

positive overflow - cannot express numbers larger than 9 x 10⁹
negative overflow - cannot express numbers smaller than -9 x 10⁹
underflow - cannot express numbers (aside from zero) between 1 x 10^-9 and -1 x 10^-9
numbers in other ranges may not be exact, since much less dense than real numbers (usually use rounding)
spacing between numbers is not constant, but percentage wise it does not vary.
relative error due to rounding always about the same.

More Realistic Floating Point

just extrapolate this same idea but to a much greater extreme when we have more digits in range and precision
increasing number of digits in fraction decreases the gap between consecutive numbers
increasing the number of digits in exponent increases the numeric ranges

Normalized Numbers

Scientific Notation suffers from lack of uniqueness

  200 x 10^-2
  20 x 10^-1
  2 x 10⁰
  0.2 x 10¹
  0.02 x 10²
  0.002 x 10³

dealing with this inside a computer can be cumbersome and costly in terms fo efficiency
since we only have a finite number of combinations, we would rpefer to have each one be a unique number and not multiple ones serving to represent the same number
having to perform essentially the same calculations on different representation increases the hardware complexity

we prefer normalized numbers, which shift fraction (and adjust exponent) to remove leading zeroes.

    34.5 x 10⁵ => 3.45 x 10⁶  
    675 x 10² => 6.75 x 10⁴  
    0.003 x 10^-6 => 3.0 x 10^-9

Binary Scientific Notation

in binary representations, exponentiation is most often to base 2 (though possibly 4, 8 or 16) rather than 10

LHS is all base 2:

  1.1 x 10⁰       = 1.5 x 2⁰    = 1.5 x 1    = 1.5
  11.01 x 10¹¹    = 3.25 x 2³   = 3.25 x 8   =  26
  101.011 x 10¹⁰⁰ = 5.375 x 2⁴  = 5.375 x 16 =  86

IEEE Standard 754

IEEE worked in the 70's to standardize floating point arithmetic
this includes both the representation and the arithmetic
remember, all finite precision arithmetic is an approximation
there are many ways to do the math approximately (some better than others)
standard defined 3 formats
1. single precision (32 bits)
2. double precision (64 bits)
3. extended precision (80 bits)
extended precision mostly used internally in hardware to reduce round-off errors (we shall speak of this no more)

IEEE 754 Representations

one bit sign (for fraction)
exponents in an "excess" representation (i.e., exponent's sign encoded in here)
radix 2 for fractions
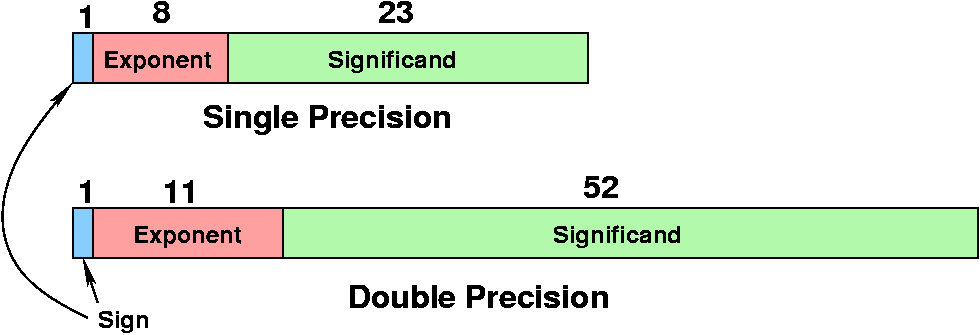
1. single precision (32 bits) - 1 sign + 8 exponent + 23 fraction (excess 127)
2. double precision (64 bits) - 1 sign + 11 exponent + 52 fraction (excess 1023)
big endian at bit level

IEEE 754 Special Cases

maximum exponents (255 and 2047) not used for normalized numbers (see below)
exponent of zero not used for normalized numbers (see below)

IEEE 754 Normalization

shift fraction so leading one is always the only digit to left of binary point
```
      e.g., 11001.001 => 1.1001001
    
```

This allows us to forego representing the binary point and let it be implicit

    1          => 1
    1.101      => 1101
    1.00001    => 100001

further,since this is binary and normalized, the 1 to the left of binary point will always be a one, so we can forego representing it as well and leave it implicit in the representation.
```
    1.0      => 0
    1.0001   => 0001
    1.1      => 1
    1.1001   => 1001
    
```
instead of calling the binary number the fraction, since there is an implied leading one and implied binary point, it is called a significand
therefore, the significand "s" is always 1 <= s < 2

IEEE 754 Examples: Normalized Numbers

     0   1000 0011   0000 0000 0000 0000 0000 000   = 1 x 2⁴ = 16

     0   0011 0001   0000 0000 0000 0000 0000 000   = 1 x 2^-78 = 3.3087e-24

     0   1000 0001   0100 0000 0000 0000 0000 000   = 1.25 x 2² = 5

IEEE 75: Handling Errors

it explicitly deals with overflow and underflow
adds four other types of numbers to the normalized numbers (total of 5 types)
- normalized
- denormalized
- zero
- infinity
- not a number

IEEE 75: Handling Underflow

IEEE 754 uses denormalized numbers to gracefully handle underflow
denormalized number exponent is 0 (really -127 or -2047)
denormalized fractional part (23 or 52 bits):
- implicit digit to left of binary point is zero
- gives only 23 significant digits rather than 24

smallest normalized number

      0   0000 0001   0000 0000 0000 0000 0000 000  = 1.0 x 2^-126 ~ 1.5 x 10^-8

largest denormalized number

      0   0000 0000   1111 1111 1111 1111 1111 111  ~ 0.99999999 x 2^-127 ~ 1.5 x 10^-8

smallest denormalized number

       0   0000 0000   0000 0000 0000 0000 0000 001  = 2^-23 x 2^-127 ~ 7 x 10^-46

the more leading zeroes in a denormalized number the less significant digits
more graceful underflow as precision rather than jumping to zero

IEEE 75: Handling Overflow

special representation for infinity
positive and negative infinity

exponent all 1's, fractional part all zeroes

   e.g.,
     0   1111 1111   0000 0000 0000 0000 0000 000   =  +Inf
     1   1111 1111   0000 0000 0000 0000 0000 000   =  -Inf

this can be used in mathematical operations

       Inf + Inf = Inf
       Inf + Inf = Inf
       Inf + C = Inf
       Inf - C = Inf
       C / 0 = Inf
       -C / 0 = -Inf
       C / Inf = 0

IEEE 754: Two Zeroes

like denormalized numbers, implicit digit to left of binary point is zero

exponent is zero, not 127 since otherwise this would be a normalized number with implicit "1" to left of binary point

  e.g.,
     0   0000 0000   0000 0000 0000 0000 0000 000   =  +0
     1   0000 0000   0000 0000 0000 0000 0000 000   =  -0

     0   0111 1111   0000 0000 0000 0000 0000 000   =  1.0 x 2⁰ = 1

+0.0 and -0.0 compare equal to each other
signed zeroes can help in determining the direction of overflow, or sign of reciprocated infinity (see below)
```
      C / Inf  = 0
      C / -Inf = 0
      1 / +0 = Inf
      1 / -0 = -Inf
  
```

IEEE 754: Not a Number (NaN)

exponent all 1's, fractional part any non-zero pattern

  e.g., 
       Inf / Inf = NaN
       0 / 0 = NaN
       sqrt( -3 ) = NaN
       cos( 2.4 ) = NaN
       log(-5) = NaN

Once NaN enters a computation, it persists through addition, subtraction, multiplication, and division.
In arithmetic comparisons, NaN is not equal to any number, including itself.
NaN is neither less than nor greater then any number.
helps defer decision about what to do with the result, instead of immediately having to handle the exceptional condition
Although IEEE 754 defines ways to deal with overflow and underflow, typically FPUs (Floating Point Processing Units) will generate exceptions so that the programmers can be informed of these conditions (if they, or the OS or compiler writers care)